Баллистика корабельной артиллерии

Современные разработки в баллистике

Поскольку боевые ракеты любого вида являются опасными для жизнедеятельности, главной задачей обороны является усовершенствование точек для запуска поражающих систем. Последние должны обеспечить полную нейтрализацию межконтинентального и баллистического оружия в любой точке движения. К рассмотрению предложена многоярусная система:

• Данное изобретение состоит из отдельных ярусов, каждый из которых имеет свое назначение: первые два будут оснащены оружием лазерного типа (самонаводящиеся ракеты, электромагнитные пушки).
• Следующих два участка оснащаются тем же оружием, но предназначенного для поражения головных частей оружия противника.

Разработки в оборонном ракетостроении не стоят на месте. Ученные занимаются модернизацией квазибаллистической ракеты. Последняя представлена как объект, имеющий низкий путь в атмосфере, но при этом резко изменяющий направление и диапазон.

Баллистическая траектория такой ракеты не влияет на скорость: даже на предельно низкой высоте объект передвигается быстрее, нежели обычный. Например, разработка РФ «Искандер» летит на сверхзвуковой скорости – от 2100 до 2600 м/с при массе 4 кг 615 г, круизы ракеты передвигают боеголовку весом до 800 кг. При полете маневрирует и уклоняется от противоракетной обороны.

Сквозные ранения

Сквозное ранение возникает при прохождении пули насквозь через тело. При этом наблюдается наличие входного и выходного отверстий. Входное отверстие небольшое, меньше калибра пули. При прямом попадании края раны ровные, а при попадании через плотную одежду под углом — с небольшим надрывом. Часто входное отверстие достаточно быстро затягивается. Следы кровотечения отсутствуют (кроме поражения крупных сосудов или при положении раны внизу). Выходное отверстие большое, может превышать калибр пули на порядки. Края раны рваные, неровные, разошедшиеся в стороны. Наблюдается быстро развивающаяся опухоль. Зачастую наблюдается сильное кровотечение. При несмертельных ранениях быстро развивается нагноение. При смертельных ранениях кожа вокруг раны быстро синеет. Сквозные ранения характерны для пуль с высоким проникающим воздействием (преимущественно для автоматных и винтовочных). При прохождении пули через мягкие ткани внутреннее ранение осевое, с небольшим повреждением соседних органов. При ранениях пулей патрона 5,45х39 (АК-74) стальной сердечник пули в теле может выйти из оболочки. В результате возникают два раневых канала и, соответственно, два выходных отверстия (от оболочки и сердечника). Такие ранения чаще всего возникают при попадании через плотную одежду (бушлат). Зачастую раневой канал от пули слепой. При попадании пули в скелет обычно возникает слепое ранение, но при большой мощности боеприпаса вероятно и сквозное. В этом случае наблюдаются большие внутренние повреждения от осколков и частей скелета с увеличением раневого канала к выходному отверстию. При этом раневой канал может «ломаться» за счет рикошета пули от скелета. Сквозные ранения в голову характеризуются растрескиванием или разломом костей черепа, часто неосевым раневым каналом. Череп растрескивается даже при попадании свинцовых безоболочечных пуль калибра 5,6 мм, не говоря уже о более мощных боеприпасах. В большинстве случаев такие ранения смертельны. При сквозных ранениях в голову часто наблюдается сильное кровотечение (длительное вытекание крови из трупа), разумеется, при положении раны сбоку или внизу. Входное отверстие довольно ровное, а выходное — неровное, с множеством растрескиваний. Смертельная рана достаточно быстро синеет и опухает. В случае растрескивания возможны нарушения кожного покрова головы. На ощупь череп легко проминается, чувствуются осколки. При ранениях достаточно сильными боеприпасами (пули патронов 7,62х39, 7,62х54) и ранениях экспансивными пулями возможно очень широкое выходное отверстие с долгим вытеканием крови и мозгового вещества.

Принцип действия

Баллистические ракеты, как правило, запускают по траектории, близкой к оптимальной, учитывая меняющиеся с высотой плотность воздуха и силу земного притяжения. Обычно ракеты стартуют вертикально для более быстрого выхода из плотных слоёв атмосферы, так как на преодоление сопротивления воздуха расходуется до 17—20 % тяги двигателя. Получив после прохода тропосферы некоторую поступательную скорость в вертикальном направлении, ракета с помощью специального программного механизма, аппаратуры и органов управления постепенно из вертикального начинает переходить в наклонное положение в сторону цели.

К концу работы двигателя продольная ось ракеты приобретает угол наклона (тангажа), отвечающий наибольшей дальности её полёта, приблизительно 45°, который уменьшается с увеличением скорости ракеты, например при скорости в 7 км/с и дальности полёта несколько более 9000 км угол наклона составляет 26°, а скорость становится равной строго установленному значению, обеспечивающему эту дальность.

При полёте по оптимальной траектории при межконтинентальной дальности ракета поднимается на высоту до тысячи и более километров и при этом видна на радиолокаторах на очень большом расстоянии. Поэтому в реальных боевых условиях могут применяться более энергозатратные настильные траектории, высота апогея которых понижена до десятков километров.

После прекращения работы двигателя весь дальнейший свой полёт ракета совершает по инерции, описывая в общем случае почти строго эллиптическую траекторию. На вершине траектории скорость полёта ракеты принимает наименьшее своё значение. Апогей траектории баллистических ракет обычно находится на высоте нескольких сотен километров от поверхности земли, где из-за малой плотности атмосферы практически полностью отсутствует сопротивление воздуха.

На нисходящем участке траектории скорость полёта ракеты за счёт потери высоты постепенно увеличивается. При дальнейшем снижении в плотные слои атмосферы ракета проходит с огромными скоростями. При этом происходит сильный разогрев обшивки баллистической ракеты, и если не будут приняты необходимые предохранительные меры, то может произойти её разрушение.

Межконтинентальное оружие: теория управления и составляющие

Многоступенчатые баллистические ракеты носят название межконтинентальных. Такое название появилось неспроста: из-за большой дальности полета становится возможным перебросить груз на другой конец Земли. Основным боевым веществом (зарядом), в основном, является атомное либо термоядерное вещество. Последнее размещается в передней части снаряда.

Далее в конструкции устанавливается система управления, двигатели и баки с топливом. Габариты и масса зависят от требуемой дальности полета: чем больше расстояние, тем выше стартовый вес и габариты конструкции.

Баллистическую траекторию полета МБР отличают от траектории иных ракет по высоте. Многоступенчатая ракета проходит процесс запуска, затем на протяжении нескольких секунд движется вверх под прямым углом. Системой управления обеспечивается направления орудия в сторону цели. Первая ступень привода ракеты после полного выгорания самостоятельно отделяется, в этот же момент запускается следующая. При достижении заданной скорости и высоты полета ракета начинает стремительно двигаться вниз к цели. Скорость полета к объекту назначения достигает 25 тыс. км/ч.

Влияние внешних факторов на полет пули

С увеличением атмосферного давления плотность воздуха увеличивается, а вследствие этого увеличивается сила сопротивления воздуха и уменьшается дальность полета пули. Наоборот, с уменьшением атмосферного давления плотность и сила сопротивления воздуха уменьшаются, а дальность полета пули увеличивается.

При повышении температуры плотность воздуха уменьшается, а вследствие этого уменьшается сила сопротивления воздуха и увеличивается дальность полета пули. Наоборот, с понижением температуры плотность и сила сопротивления воздуха увеличиваются, и дальность полета пули уменьшается.

При попутном ветре уменьшается скорость полета пули относительно воздуха. С уменьшением скорости полета пули относительно воздуха сила сопротивления воздуха уменьшается. Поэтому при попутном ветре пуля полетит дальше, чем при безветрии.

При встречном ветре скорость пули относительно воздуха будет больше, чем при безветрии, следовательно, сила сопротивления воздуха увеличится, и дальность полета пули уменьшится.

Продольный (попутный, встречный) ветер на полет пули оказывает незначительное влияние, и в практике стрельбы из стрелкового оружия поправки на такой ветер не вводятся.

Боковой ветер оказывает давление на боковую поверхность пули и отклоняет ее в сторону от плоскости стрельбы в зависимости от его направления: ветер справа отклоняет пулю в левую сторону, ветер слева – в правую сторону.

Влияние внешних факторов на полет пули

Скорость ветра определяется с достаточной точностью по простым признакам: при слабом ветре (2-3 м/сек) носовой платок и флаг колышутся и слегка развеваются; при умеренном ветре (4-6 м/сек) флаг держится развернутым, а платок развевается; при сильном ветре (8-12 м/сек) флаг с шумом развевается, платок рвется из рук и т. д.

Скорость ветра

Изменение влажности воздуха оказывает незначительное влияние на плотность воздуха и, следовательно, на дальность полета пули, поэтому оно не учитывается при стрельбе.

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t\ $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.

Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.

Нормальные (табличные) условия стрельбы

Табличные данные траектории соответствуют нормальным условиям стрельбы.

За нормальные (табличные) условия приняты следующие:

Метеорологические условия:

• атмосферное (барометрическое) давление на горизонте оружия 750 мм рт. ст.;
• температура воздуха на горизонте оружия +15° С;
• относительная влажность воздуха 50% (относительной влажностью называется отношение количества водяных паров, содержащихся в воздухе, к наибольшему количеству водяных паров, которое может содержаться в воздухе при данной температуре);
• ветер отсутствует (атмосфера неподвижна).

Баллистические условия:

• вес пули, начальная скорость и угол вылета равны значениям, указанным в таблицах стрельбы;
• температура заряда +15°С;
• форма пули соответствует установленному чертежу;
• высота мушки установлена по данным приведения оружия к нормальному бою;
• высоты (деления) прицела соответствуют табличным углам прицеливания.

Топографические условия:

• цель находится на горизонте оружия;
• боковой наклон оружия отсутствует.

При отклонении условий стрельбы от нормальных может возникнуть необходимость определения и учета поправок дальности и направления стрельбы.

Ракетные комплексы и установки заграничной оборонной промышленности

Высота баллистической траектории ракеты американского комплекса «Минитмен-3» не особо отличается от характеристик полета отечественных изобретений.

Комплекс, который разработан в США, является единственным «защитником» Северной Америки среди оружия такого вида до сегодняшнего дня. Несмотря на давность изобретения, показатели устойчивости орудия являются неплохими и в нынешнее время, ведь ракеты комплекса могли противостоять противоракетной обороне, а также поразить цель с высоким уровнем защиты. Активный участок полета непродолжительный, и составляет 160 с.

Другое изобретение американцев – «Пискипер». Он также мог обеспечить точное попадание в цель благодаря наивыгоднейшей траектории баллистического движения. Специалисты утверждают, что боевые возможности приведенного комплекса почти в 8 раз выше, нежели у «Минитмена». Боевое дежурство «Пискипера» составляло 30 секунд.

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения x(t) = x0 + v0xt + axt^2/2 x(t) — искомая координата x0 — начальная координата v0x — начальная скорость тела в данный момент времени [м/с] t — время ax — ускорение [м/с^2]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости →          → v = v0 + at → v — конечная скорость тела [м/с] v0 — начальная скорость тела [м/с] t — время → a — ускорение [м/с^2]

Задача

Найдите местоположение автобуса через 0,5 часа после начала движения, разогнавшегося до скорости 60 км/ч за 3 минуты.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

v = v0 + at
a = v — v0 / t

Так как автобус двигался с места, v0 = 0. Значит
a = v/t

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч^2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt^2/2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

x(t) = axt^2/2

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
x = 1200*0,5^2/2 = 1200*0,522= 150 км

Ответ: через полчаса координата автобуса будет равна 150 км.

Полет снаряда и движение в атмосфере

Из раздела динамики известно влияние плотности воздуха на скорость передвижения любого тела в различных слоях атмосферы. Функция последнего параметра учитывает зависимость плотности непосредственно от высоты полета и выражается в зависимости:

Н_(у)=20000-у/20000+у;

где у – высота полета снаряда (м).

Расчет параметров, а также траектории межконтинентальной баллистической ракеты можно производить с помощью специальных программ на ЭВМ. Последние приведут ведомости, а также данные о высоте полета, скорости и ускорении, продолжительности каждого этапа.

Экспериментальная часть подтверждает расчетные характеристики, и доказывает, что на скорость оказывает влияние форма снаряда (чем лучше обтекаемость, тем выше скорость).

Примеры задач с решением

Пример 1

Задание: Точка движется в плоскости XOY из начала координат со скоростью $\overline{v}=A\overline{i}+Bx\overline{j}\ ,\ $где $\overline{i}$, $\overline{j}$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. \textit{}

Решение: Рассмотрим уравнение изменения скорости частицы:

\

Из этого уравнения следует, что:

\

Из (1.2) имеем:

\

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

\

Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:

\

   

Пример 2

Задание: Движение материальной точки в плоскости описывает система уравнений: $\left\{ \begin{array}{c}
x=At. \\
y=At(1+Bt) \end{array}
\right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

\

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

\

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

\

Ответ: $y=x+\frac{B}{A}x^2$

Секущие ранения

Секущие ранения наблюдаются при попадании пули в тело под острым углом с нарушением только кожного покрова и внешних частей мышц. В большинстве своем ранения неопасные. Характеризуются разрывом кожи; края раны неровные, рваные, часто сильно расходятся. Иногда наблюдается достаточно сильное кровотечение, особенно при разрыве крупных подкожных сосудов.

Баллистика. Огневая подготовка в охранном предприятии

Баллистика. Огневая подготовка в охранном предприятии Стрельба из служебных пистолетов и револьверов Е.Б. Ефимов, Ю.Н.Буряк Общие сведения о баллистикеБАЛЛИСТИКА — наука о движении снарядов. В свою очередь, баллистику разделяют на две части: внутреннюю и…

История баллистики

После окончания Франко-Прусской войны в Германии концерн «Friedrich Krupp AG» под руководством Альфреда Круппа стал систематизировать и обрабатывать данные о влиянии воздуха на движение и смещение движущегося снаряда, надо заметить что в этот период данное…

Как выполняется расчет: упрощенная формула

Для того чтобы определить, где именно на земле взорвется ракета, специалисты производят расчеты с использованием методики интегрирования и дифференциальных уравнений. Подобные вычисления обычно отличаются сложностью и дают максимально точные результаты попадания.

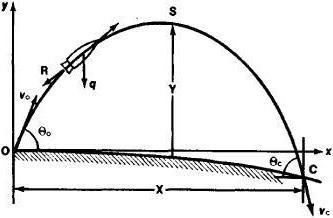
Иногда для расчетов баллистической траектории ракет может использоваться и упрощенная методика. Воздух на границе атмосферы, как известно, разреженный. А поэтому его сопротивление для баллистических ракет иногда может не учитываться. Выглядит упрощенная формула расчета баллистической траектории следующим образом:

y=x-tgѲ0-gx2/2V02-Cos2Ѳ0, где:

x — расстояние от точки вылета до вершины пути, y — вершина траектории, v0 — скорость при запуске, Ѳ0 — угол запуска. Путь объекта в данном случае представляет собой параболу. Называется такая траектория вакуумной.

Если сопротивления воздуха при полете баллистической ракеты будет учтено, формулы получатся очень сложными. Выполнять же такие длительные расчеты зачастую бывает нецелесообразным, поскольку погрешность, возникающая из-за влияния атмосферы в разреженном воздухе, незначительна и особой роли не играет.

Скорости и система отсчета

Проезжающий самолет со скоростью (красный), радиальной скоростью (зеленый) и тангенциальной скоростью (синий)

В зависимости от используемой системы отсчета или системы координат были установлены различные термины:

Декартова система координат часто используется в однородном гравитационном поле . Скорости , которые направлены параллельно ускорению свободного падения , обычно называют вертикальными скоростями , а скорости , которые ортогональны этому направлению, называют горизонтальными скоростями .
грамм→{\ displaystyle {\ vec {g}}}

В случае полярных координат радиальная скорость является составляющей вектора скорости в направлении вектора положения , то есть вдоль соединительной линии между движущимся объектом и началом координат. Компонент, перпендикулярный этому, называется периферийной скоростью . : Таким образом результаты . Векторное произведение от угловой скорости и вектор положения приводит к окружной скорости : .
v→р{\ displaystyle {\ vec {v}} _ {\ mathrm {r}}} v→⊥{\ displaystyle {\ vec {v}} _ {\ perp}}v→знак равноv→⊥+v→р{\ displaystyle {\ vec {v}} = {\ vec {v}} _ {\ perp} + {\ vec {v}} _ {\ mathrm {r}}}v→⊥знак равноω→×р→{\ displaystyle {\ vec {v}} _ {\ perp} = {\ vec {\ omega}} \ times {\ vec {r}}}

При движении по круговой траектории вокруг начала координат, но только в этом случае, радиальная скорость равна нулю, а окружная скорость равна тангенциальной скорости, то есть скорости траектории по касательной к кривой траектории.

Из изменения расстояния до начала координат (радиуса) следует радиальная скорость .
v→рзнак равнор˙р→|р→|{\ displaystyle {\ vec {v}} _ {\ mathrm {r}} = {\ dot {r}} \, {\ frac {\ vec {r}} {| {\ vec {r}} |}} }

Если предположить, что существует общепризнанная система отсчета, скорости, которые измеряются в этой системе, называются абсолютными скоростями . Скорости, относящиеся к движущейся точке в этой системе, называются относительными скоростями . Пример: трамвай движется со скоростью 50 км / ч. В нем пассажир движется с относительной скоростью (по сравнению с трамваем) 5 км / ч. Его абсолютная скорость (с точки зрения неподвижного наблюдателя на дороге) составляет 55 км / ч или 45 км / ч, в зависимости от того, движется ли он в направлении движения или против направления движения.

Однако принцип относительности гласит, что нет физической причины, по которой следует выделить определенную систему отсчета и предпочесть ее другим системам. Все физические законы, действующие в одной инерциальной системе, применимы и во всех других. Какие движения считаются «абсолютными» — совершенно произвольно. Вот почему концепции абсолютной скорости избегают, самое позднее, со времен специальной теории относительности . Вместо этого все скорости являются относительными. Из этого принципа относительности вместе с скорости света следует, что скорости — как неявно предполагается в приведенном выше примере — нельзя просто сложить. Вместо этого к скоростям применяется релятивистская теорема сложения . Однако это заметно только на очень высоких скоростях.

Ракеты: особенности запуска и движения

Различают управляемые и неуправляемые баллистические ракеты. На формирование траектории также влияют внешние и наружные факторы (силы сопротивления, трения, вес, температура, требуемая дальность полета и т.д).

Общий путь запущенного тела можно описать следующими этапами:

• Запуск. При этом ракета переходит в первую стадию и начинает свое движение. С этого момента и начинается измерение высоты траектории полета баллистической ракеты.
• Приблизительно через минуту запускается второй двигатель.
• Через 60 секунд после второго этапа запускается третий двигатель.
• Далее тело входит в атмосферу.
• В последнюю очередь происходит взрыв боевых головок.

Примечания

1.  (англ.). GlobalSecurity.org. Дата обращения: 22 августа 2012.
2. Николаев Леонид. . Сайт «Военный паритет» (3 мая 2007). Дата обращения: 22 августа 2012.
3. Charles P. Vick.  (англ.). GlobalSecurity (20 March 2007). Дата обращения: 18 мая 2012.
4. Жидкотопливная ракета «Титан-II» осталась на вооружении только потому, что лишь она могла нести 9-мегатонные боевые части, слишком тяжёлые для «Минитмена»
5. ↑  (недоступная ссылка). Дата обращения: 3 ноября 2013.
6.  (недоступная ссылка). Дата обращения: 3 ноября 2013.
7.  (недоступная ссылка). Дата обращения: 3 ноября 2013.
8.  (недоступная ссылка). Дата обращения: 3 ноября 2013.
9. . Дата обращения: 3 ноября 2013.

Решение баллистических задач

Для этого полезно изготовить график зависимости смещения (рассеивания, времени полета пули) от дальности стрельбы. Такой график позволит легко вычислять промежуточные значения (например, на 350 м), а также позволит предположить затабличные значения функции. На рис. 18 представлена простейшая баллистическая задача.
Стрельба ведется на дистанцию 600 м, ветер под углом 45° к траектории дует сзади-слева. Вопрос: диаметр круга рассеивания и смещение его центра от цели; время полета до цели.
Решение: Диаметр круга рассеивания 48 см (см. табл. 3). Деривационное смещение центра — 12 см вправо (см. табл. 4). Смещение пули ветром — 115 см (110*2/2 + 5% (за счет направления ветра по направлению деривационного смещения)) (см. табл. 5). Время полета пули — 1,07 с (время полета + 5% за счет направления ветра по направлению полета пули)(см.табл. 6).
Ответ; пуля пролетит 600 м за 1,07 с, диаметр круга рассеивания будет равен 48 см, причем его центр сместится вправо на 127 см. Естественно, данные ответа достаточно приблизительны, но их расхождение с реальными данными не более 10%.

Причины деривации и ее значение

Деривация пули всегда направлена в ту сторону, в которую проходят стволовые нарезки. В связи с тем, что все современные модели нарезного оружия имеют нарезы в направлении слева – вверх — направо (за исключением стрелкового оружия Японии), то отклонение пули, снаряда осуществляется в правую сторону.

Деривация растет относительно дистанции стрельбы непропорционально. Вместе с увеличением дальность полета пули, деривация имеет тенденцию к постепенному росту. Поэтому траектория пули, если смотреть на нее сверху, являет собой линию, у которой кривизна постоянно нарастает.

При стрельбе на расстоянии в 1 км деривация оказывает существенное влияние на отклонение пули. Так в стандартных справочниках таблица 3 пули 7,62 х 39 деривацию показывает в размере порядка 40-60 см. Однако многочисленные исследования специалистов в области баллистики приводят к выводу, что деривацию следует учитывать только на дистанциях более 300 м.

Современная артиллерия деривационные поправки учитывает автоматически, либо посредством использования таблиц стрельбы. Отдельные образцы стрелкового оружия снабжаются оптическими прицелами, в которых она учитывается конструктивно. Прицелы монтируются таким образом, что при выстреле пуля автоматически уходит немного левее. При достижении дистанции в 300 м она оказывается на пристреливаемой линии.

Смещение пули ветром

Среди всех сторонних условий, влияющих на полет пули (влажность, давление и т. д.), необходимо выделить наиболее серьезный фактор — влияние ветра. Ветер достаточно серьезно сносит пулю, особенно в конце восходящей ветви траектории и далее. Смещение пули боковым ветром (под углом 900 к траектории) средней силы (6-8 м/с) показано в табл. 5.
Таблица 5
Смещение пули ветром

Дальность огня (м)

Для выяснения смещения пули сильным ветром (12-16 м/с) необходимо удвоить значения таблицы, для слабого ветра (3-4 м/с) табличные значения делят пополам. Для ветра, дующего под углом 45° к траектории, табличные значения также делятся пополам.