§ 15. географические координаты

Астрономические координаты

Как определять широту и долготу точки с большой точностью – эта задача становится все более сложной по мере увеличения масштаба. Дело в том, что расхождения между реальной формой Земли и ее сферической моделью проявляются гораздо явственнее на мелко масштабированных картах. Для таких случаев применяется астрономическая система координат, учитывающая настоящую форму планеты.

В связи с тем, что планета вращается с достаточно большой скоростью, ее внутреннее вещество в виде жидкой мантии испытывает на себе центробежную силу. Она вытягивает планету у экватора и стягивает у полюсов. Поэтому радиус Земли в этих 2-х точках различен: 6357 км от центра планеты до полюса и 6378 км от центра до экватора.

Здесь заключается главное отличие астрономической системы координат от сферической. В первой линия — которую в этой системе называют отвесной линией — от точки параллельна направлению силы тяжести и перпендикулярна земной поверхности, а во второй – к центру планеты.

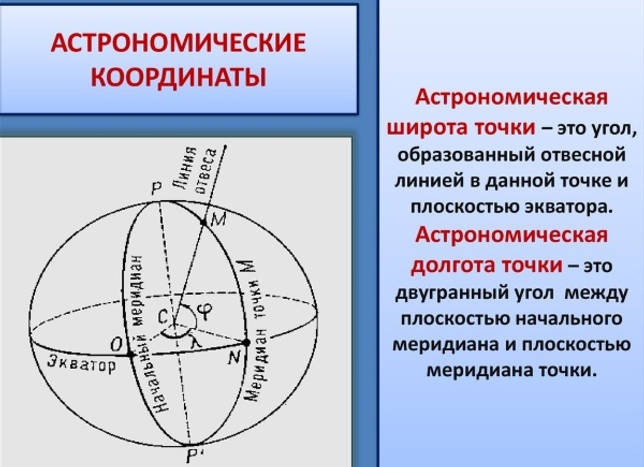
Для определения отвесной линии применяются астрономические наблюдения за небесной сферой с помощью специальных инструментов либо математические вычисления на основе этих наблюдений. Для каждого региона она будет различна, так как вещество внутри планеты распределено неравномерно.

Формулы плоской поверхности

Планарное приближение для поверхности Земли может быть полезно на небольших расстояниях. Точность вычислений расстояний с использованием этого приближения становится все более неточной, так как:

• Расстояние между точками становится больше;
• Точка становится ближе к географическому полюсу.

Кратчайшее расстояние между двумя точками на плоскости — прямая. Теорема Пифагора используется для вычисления расстояния между точками на плоскости.

Даже на небольших расстояниях точность вычислений географических расстояний, предполагающих наличие плоской Земли, зависит от метода, с помощью которого координаты широты и долготы проецируются на плоскость. Проекция координат широты и долготы на плоскость — это область картографии .

Формулы, представленные в этом разделе, обеспечивают разную степень точности.

Сферическая Земля в проекции на самолет

Эта формула учитывает изменение расстояния между меридианами в зависимости от широты:

D знак равно р ( Δ ϕ ) 2 + ( потому что ⁡ ( ϕ м ) Δ λ ) 2 , {\ displaystyle D = R {\ sqrt {(\ Delta \ phi) ^ {2} + (\ cos (\ phi _ {m}) \ Delta \ lambda) ^ {2}}},}

где:

Δ ϕ {\ displaystyle \ Delta \ phi \, \!} и указаны в радианах; Δ λ {\ displaystyle \ Delta \ lambda \, \!}

ϕ м {\ Displaystyle \ phi _ {м} \, \!} должны быть в единицах, совместимых с методом, используемым для определения потому что ⁡ ( ϕ м ) . {\ Displaystyle \ соз (\ фи _ {м}). \, \!}

Чтобы преобразовать широту или долготу в радианы, используйте

1 ∘ знак равно ( π 180 ) р а d я а п s . {\ displaystyle 1 ^ {\ circ} = (\ pi / 180) \, \ mathrm {радианы}.}

Это приближение очень быстрое и дает довольно точный результат для небольших расстояний. Кроме того, при упорядочивании местоположений по расстоянию, например, в запросе к базе данных, быстрее выполняется сортировка по квадрату расстояния, что устраняет необходимость в вычислении квадратного корня.

Эллипсоидальная Земля в проекции на плоскость

FCC предусматривает следующие формулы для расстояний , не превышающих 475 километров (295 миль):

D знак равно ( K 1 Δ ϕ ) 2 + ( K 2 Δ λ ) 2 , {\ displaystyle D = {\ sqrt {(K_ {1} \ Delta \ phi) ^ {2} + (K_ {2} \ Delta \ lambda) ^ {2}}},}

где

D {\ Displaystyle D \, \!} = Расстояние в километрах;

Δ ϕ {\ displaystyle \ Delta \ phi \, \!} и находятся в градусах; Δ λ {\ displaystyle \ Delta \ lambda \, \!}

ϕ м {\ Displaystyle \ phi _ {м} \, \!} должны быть в единицах, совместимых с методом, используемым для определения потому что ⁡ ( ϕ м ) ; {\ Displaystyle \ соз (\ фи _ {м}); \, \!}

K 1 знак равно 111,13209 — 0,56605 потому что ⁡ ( 2 ϕ м ) + 0,00120 потому что ⁡ ( 4 ϕ м ) ; K 2 знак равно 111,41513 потому что ⁡ ( ϕ м ) — 0,09455 потому что ⁡ ( 3 ϕ м ) + 0,00012 потому что ⁡ ( 5 ϕ м ) . {\ displaystyle {\ begin {align} K_ {1} & = 111.13209-0.56605 \ cos (2 \ phi _ {m}) + 0,00120 \ cos (4 \ phi _ {m}); \\ K_ {2} & = 111,41513 \ cos (\ phi _ {m}) — 0,09455 \ cos (3 \ phi _ {m}) + 0,00012 \ cos (5 \ phi _ {m}). \ End {align}} \, \!}

Где и выражены в километрах на градус. Интересно отметить, что:
K 1 {\ displaystyle K_ {1}} K 2 {\ displaystyle K_ {2}}

K 1 знак равно M π 180 {\ displaystyle K_ {1} = M {\ frac {\ pi} {180}} \, \!} = километров на градус разницы широты;

K 2 знак равно потому что ⁡ ( ϕ м ) N π 180 {\ displaystyle K_ {2} = \ cos (\ phi _ {m}) N {\ frac {\ pi} {180}} \, \!} = километров на градус разницы долготы;

где и являются м eridional и его перпендикулярен, или « п НПУ », (выражения в формуле FCC являются производными от биномиальной серии формы расширения и , набора к Кларку 1866 г. эллипсоиду ). M {\ Displaystyle M \, \!} N {\ Displaystyle N \, \!} M {\ Displaystyle M \, \!} N {\ Displaystyle N \, \!}

Для более эффективной с вычислительной точки зрения реализации вышеприведенной формулы несколько приложений косинуса можно заменить одним приложением и использованием рекуррентного соотношения для полиномов Чебышева .

Формула плоской Земли в полярных координатах

D знак равно р θ 1 2 + θ 2 2 — 2 θ 1 θ 2 потому что ⁡ ( Δ λ ) , {\ displaystyle D = R {\ sqrt {\ theta _ {1} ^ {2} \; {\ boldsymbol {+}} \; \ theta _ {2} ^ {2} \; \ mathbf {-} \; 2 \ theta _ {1} \ theta _ {2} \ cos (\ Delta \ lambda)}},}

где значения ширины в радианах. Для широты, измеряемой в градусах, широта в радианах может быть вычислена следующим образом: θ знак равно π 180 ( 90 ∘ — ϕ ) . {\ displaystyle \ theta = {\ frac {\ pi} {180}} (90 ^ {\ circ} — \ phi). \, \!}

Правила определения долготы и широты

Из всего написанного выше можно сделать вывод, что для определения координат по карте решающую роль играют широта и долгота, поэтому крайне важно научиться определять их. Сначала остановимся на широте

Нулевой точкой отсчета здесь считается экватор с нулевым градусом. От него к полюсам расходятся параллели. На полюсе широта составляет 90 градусов, а все точки, расположенные на равном удалении от экватора в сторону одного из полюсов, имеют одинаковую северную или южную широту (например, 20, 40 или 60 градусов). При этом, чем дальше объект на карте от экватора и ближе к полюсу, тем больше будет его широта (рисунок 4)

Сначала остановимся на широте. Нулевой точкой отсчета здесь считается экватор с нулевым градусом. От него к полюсам расходятся параллели. На полюсе широта составляет 90 градусов, а все точки, расположенные на равном удалении от экватора в сторону одного из полюсов, имеют одинаковую северную или южную широту (например, 20, 40 или 60 градусов). При этом, чем дальше объект на карте от экватора и ближе к полюсу, тем больше будет его широта (рисунок 4).

Рисунок 4. Схемы определения широты и долготы

Географическая долгота на картах и глобусах отсчитывается от меридиана в Гринвиче, который считается нулевым. Здесь, как и в случае с широтой, удаление от этого меридиана приводит и к увеличению долготы. При этом максимальный показатель долготы составляет 180 градусов, поскольку полная окружность сферы (восточного и западного полушария) составляет 360 градусов.

Чтобы определить по карте географические координаты объекта, нужно сделать следующее:

1. Определить, в каком полушарии находится точка, в северном или южном. Если выше экватора, то широта будет северной, а если ниже – южной.
2. Далее нужно посмотреть, между какими параллелями располагается точка. Градусы параллелей обычно указаны сбоку карты.
3. Теперь необходимо подсчитать количество градусов от ближайшей со стороны экватора параллели к заданной точке.
4. Далее переходим к определению долготы. Здесь отсчет ведется от нулевого меридиана в Гринвиче. Если точка расположена слева от него, то точка находится в западном полушарии, а если справа – в восточном.
5. Теперь находим, между какими меридианами находится точка, и, как и в случае с широтой, подсчитываем количество градусов до ближайшего со стороны Гринвича меридиана.

В результате вы получите точную широту и долготу, а также определенное количество градусов для каждого показателя, которые уточняют расположение объекта.

Координаты городов России и стран мира в таблице

Чтобы узнать, где расположено нужное вам место, можно также воспользоваться специальными картами и таблицами онлайн. Это — самое простое решение, ведь не надо будет самостоятельно высчитывать и находить по адресу интересующий вас объект.

Таблица 1. Координаты городов России

Таблица 2 . Координаты стран мира

Геокоординаты не только помогают морякам, пилотам, исследователям ориентироваться в пути при отсутствии видимости или нахождении в пространстве без каких-либо опознавательных знаков. Имея знания и понимание принципов расчета, можно применить эти знания на практике, например, пользуясь компасом в турпоходе и ориентируясь по координатам в длительных путешествиях.

Предыдущая

ГеографияПриродные зоны России — виды с названиями и описанием

Следующая

ГеографияСостав воздуха — химическая формула, концентрация веществ

Это интересно: Что такое азимут и как его определить?

Определение географических координат широты на карте мира: пример

Определение географических координат широты на карте мира: пример

Как говорилось выше, широта — это параллели. Чтобы ее определить нужно провести линию, параллельную экватору или близлежащей параллели.

• Если объект находится на самой параллели, то определить его местонахождение просто (было описано выше).
• Если объект находится между параллелями, тогда его широта определяется по ближайшей параллели от экватора.
• Например, Москва находится севернее 50-й параллели. По меридиану отмеряется расстояние до этого объекта и оно равно 6°, значит, у Москвы географическая широта равна 56°.

Наглядный пример определения географических координат широты на карте мира можно найти в нижеследующем видео:

Меридиан

Меридианом в географии называют половину линии сечения земной поверхности, проведённой через земную ось вращения и любую точку на поверхности. Все воображаемые меридианы, которых может быть бесконечное количество, соединяются на полюсах — Северном и Южном. Протяжённость каждого из них — 20 004 276 метров.

Хотя меридианов мысленно можно провести как угодно много, для удобства передвижения, составления карт их количество, расположение упорядочили международными договорами. В 1884 году на Международной меридианной конференции в Вашингтоне постановили, что начальным меридианом (нулевым) станет тот, что проходит через Гринвич — округ на юго-востоке Лондона.

Однако не все сразу согласились с таким решением. Например, в России даже после 1884 года вплоть до начала ХХ века нулевым меридианом считали собственный — Пулковский: он «проходит» через Круглый зал Пулковской обсерватории.

Градусная сеть, ее элементы. Географические координаты — Гипермаркет знаний

Гипермаркет знаний>>География>>География 6 класс>> Градусная сеть, ее элементы. Географические координаты

§ 3. Градусная сеть, ее элементы. Географические координаты

Ориентироваться по карте и находить точное местоположение географических объектов на поверхности Земли позволяет градусная сеть, или система линий параллелей и меридианов.

Параллели (от греч. parallelos — букв, идущий рядом) — это линии, условно проведенные на поверхности Земли параллельно экватору. Параллелей на карте и глобусе можно провести сколько угодно, но обычно на учебных картах их проводят с интервалом 10—20°. Параллели всегда ориентированы с запада на восток. Длина окружности параллелей уменьшается от экватора к полюсам.

Экватор (от лат. aequator — уравнитель) — воображаемая линия на земной поверхности, полученная при мысленном рассечении Земного шара плоскостью, проходящей через центр Земли перпендикулярно оси ее вращения. Все точки на экваторе оказываются равноудаленными от полюсов. Экватор делит Земной шар на два полушария — Северное и Южное.

Меридиан (от лат. meridians — полуденный) — кратчайшая линия, условно проведенная поверхности Земли от одного полюса до другого.Таблица 2

                          Сравнительная характеристика меридианов и параллелей

Признаки	Меридианы	Параллели
Направление	С.-Ю.	З.-В.
Название нулевой линии	Гринвичский (Лондонский) меридиан	Экватор
Длина, км	20 000	От 40 000 до 0
Длина одного градуса, км	111	От 111 до 0
Форма на глобусе	Полуокружность	Окружности
Форма на карте полушарий	Срединные меридианы — прямые, остальные — дуги	Экватор — прямая, остальные — дуги

Географические полюсы (от лат. polus — ось) — математически высчитанные точки пересечения воображаемой оси вращения Земли с земной поверхностью. Меридианы можно провести через любые точки на земной поверхности, и все они будут проходить через оба полюса Земли.

Меридианы ориентированы с севера на юг, и все имеют одинаковую длину (от полюса до полюса) — около 20000 км. Средняя длина 1° меридиана: 20004 км : 180° = 111 км. Направление местного меридиана в любой точке можно определить в полдень по тени от любого предмета.

В Северном полушарии конец тени всегда показывает направление на север, в Южном полушарии — на юг.

Градусная, или картографическая, сеть служит для определения географических координат точек земной поверхности — долгот и широт — или нанесения на карту объектов по их координатам. Все точки данного меридиана имеют одну и ту же долготу, а все точки параллели — одинаковую широту. 

Географическая широта — это величина дуги меридиана в градусах от экватора до заданной точки. Так, Санкт-Петербург находится в Северном полушарии, на 60° северной широты (сокращенно с.ш.

), Суэцкий канал — на 30° с.ш. Определить географическую широту любой точки на глобусе или карте — это определить, на какой параллели она находится.

К югу от экватора любая точка будет иметь южную широту (сокращенно ю. ш.).

Географическая долгота — это величина дуги параллели в градусах от начального меридиана до заданной точки. Начальный, или нулевой, меридиан выбран условно и проходит через Гринвичскую обсерваторию, находящуюся недалеко от Лондона. К востоку от этого меридиана определяется восточная долгота (в. д.), к западу — западная (з.д.) (рис. 10).

Широта и долгота любой точки Земли составляют ее графические координаты. Так, географические координаты Москвы — 56° с.ш. и 38° в. д.

Максаковский В.П., Петрова Н.Н., Физическая и экономическая география мира. — М.:Айрис-пресс, 2010. — 368с.:ил.

Видеопо географии скачать, домашнее задание, учителям и школьникам на помощь онлайн

Содержание урока конспект урока
опорный каркас презентация урока
акселеративные методы интерактивные технологии Практика
задачи и упражнения самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа
фотографии, картинки графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения рефераты
статьи фишки для любознательных шпаргалки учебники основные и дополнительные
словарь терминов прочие
Совершенствование учебников и уроков исправление ошибок в учебнике
обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки
календарный план на год методические рекомендации программы
обсуждения Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

3D декартовы координаты

Каждая точка, выраженная в эллипсоидальных координатах, может быть выражена как прямолинейная xyz ( декартова ) координата. Декартовы координаты упрощают многие математические вычисления. Декартовы системы разных датумов не эквивалентны.

В центре Земли, фиксировано на Земле

Земля по центру, фиксированные координаты Земли относительно широты и долготы.

Геоцентрическая Земля фиксированная (также известный как ECEF, ECF, или обычные наземные системы координат) вращается с Землей , и имеет свое начало в центре Земли.

Обычная правая система координат ставит:

• Начало координат в центре масс Земли, точка, близкая к центру фигуры Земли.
  
• Ось Z на линии между Северным и Южным полюсами с положительными значениями, увеличивающимися к северу (но не совсем совпадает с осью вращения Земли)
• Оси X и Y в плоскости экватора
• Ось X, проходящая через нее, простирается от 180 градусов долготы на экваторе (отрицательное значение) до 0 градусов долготы ( ) на экваторе (положительное значение).
• Ось Y, проходящая через нее, простирается от 90 градусов западной долготы на экваторе (отрицательное значение) до 90 градусов восточной долготы на экваторе (положительное значение).

Местная касательная плоскость

Земля по центру Земля фиксированная, координаты — восток, север, верх.

Локальная касательная плоскость может быть определена на основе вертикальных и горизонтальных размеров. Вертикальная координата может указывать либо вверх , либо вниз. Для рамок существует два вида условных обозначений:

• Восток, Север, вверх (ЕНУ), используется в географии
• Север, восток, вниз (NED), используется специально в аэрокосмической отрасли

Во многих приложениях для наведения и отслеживания местная декартова система координат ENU гораздо более интуитивно понятна и практична, чем ECEF или геодезические координаты. Локальные координаты ENU формируются из плоскости, касательной к поверхности Земли, привязанной к определенному месту, и поэтому ее иногда называют местной касательной или локальной геодезической плоскостью. Условно обозначена восточная ось — север и верх .
Икс{\ displaystyle x}у{\ displaystyle y}z{\ displaystyle z}

В самолете большинство интересных объектов находится под ним, поэтому разумно определить «вниз» как положительное число. Координаты NED позволяют это в качестве альтернативы ENU. Условно обозначена северная ось , восток и вниз . Чтобы избежать путаницы между и и т. Д., В этой статье мы ограничим локальную систему координат до ENU.
Икс′{\ displaystyle x ‘}у′{\ displaystyle y ‘}z′{\ displaystyle z ‘}Икс{\ displaystyle x}Икс′{\ displaystyle x ‘}

LatLong.ru

Пересчет географических координат. Градусы -> градусы/минуты/секунды:

Пересчет географических координат. Градусы/минуты/секунды -> градусы: Определение высоты над уровнем моря по координатам: Форма поиска географических координат объекта на основе картографических сервисов Google или Yandex.

Примеры:

Москва Новгородская обл., Бердск Санкт-Петербург, Дворцовая наб., 38 55.7522,37.6156 (широта,долгота)

Недавно искали: N 59,6099 E16,5448 (yandex) 59 19 45 с.ш. 18 04 07 в.д (yandex) Galinės 1, Galinės k., Avižienių sen, LT-14247 Vilniaus r. (yandex) 55° 45.2376′ 0» N,37° 37.2236′ 0» E (yandex) X 459694.14 Y 1249991.18 (yandex) X 716339.96 Y 1497441.41 (yandex) 43.684485 N 40.256234E (yandex) 55,753396 37,549588 (yandex) 52 с.ш 36 в.д (yandex) Свердловская область географические координаты 57.48 2СШ 60.3 14ВД (yandex)

N:51,723950, E:39,249170 (yandex) 43°31’42.8 N / 8°12’05.2 W (yandex) ск 42 (yandex) 45.281647 с.ш 38.357707 в.д (yandex) 56 с.ш 43 в.д (yandex) широта 44.33.2489 долгота 33.47.26.5099 (yandex) 53.218469, 50.274046 (yandex) 51° 09′ 45.1»N 43° 25′ 08.2» E (yandex) 46.579748 N 39.669957 E (yandex) Иркутская область байкальск (yandex)

Долгота:49°10′52.68″E (49,181300) Широта:55°54′58.68″N (55,916300) (yandex) 52 28 46 N, 62 11 08 E (yandex) 59,9402472, 30,4381927 (yandex) N 56.464°E 84.9625° (yandex) Вологодская область ФАД А-114 97.7 (yandex) 55.7558°,55.7558° (yandex) 60.7710, 28.7787 (yandex) широта- 44,66401 долгота-41,90238 (yandex) АВТОДОРОГА ЕКАТЕРИНБУРГ-Н.ТАГИЛ-СЕРОВ 126.400 КМ (ИЗ ЕКАТЕРИНБУРГА) (yandex) 164 километр автодороги воронеж- тамбов (yandex)

34°57 ‘ ю.ш. 150°30 ‘ в.д. (yandex) 63° 11.55 N,74° 36.42 E (yandex) гора Аксоран (yandex) N55.795773, e52.499207 (yandex) 55°58.38 S 67°15.46 W (yandex) 150°30 43 ‘ ю.ш. 34 57 23 ‘ в.д. (yandex) lat 42.683 lon 23.318 (yandex) Широта 53.883369 Долгота 51.236328 (yandex) 51.5333, 46.0345саратов, Саратовская область (yandex) 55deg 47.48916 ‘ N, 37deg 32.94132 ‘ E (yandex)

X 1380050.49 Y 392592.35 (yandex) 59.4928981 29.7625919 (yandex) 56.000326, 37.543188 (yandex) Широта 55.7483 Долгота 37.6171 (yandex) N55.652220 E52.247437 (yandex) N55.7558°E55.7558° (yandex) г. Костанай, ул. Гоголя, д. 79а (yandex) N61.214030,E73.160690 (yandex) N+E+ (yandex) 577917,3500 2350652,2500 (yandex)

N 53.2022° E 50.1596° (yandex) N E 44,923202 37,325763 (yandex) любытинский район (yandex) Екатеринбург57 5.2 сш 60 23.19 вд (yandex) N 45.0421° E 38.9806° краснодар (yandex) n55 38,094 e37 55,743 (yandex) N:44,923202 E:37,325763 (yandex) Широта 55.7578 Долгота 55.7578 (yandex) E8.05282006 N45.56579763 (yandex) 55,558741° с.ш., 37,378847° в.д. (55°33ʹ31,46ʺ с.ш., 37°22ʹ43,84ʺ в.д.) (yandex)

48.473692,44.537359 Волгоградская область, г.Волгоград, Светлоярский район (yandex) N 55.0392° E 82.9278° (yandex) 83.0335, 54.9022 (yandex) село Заря Якшур-Бодьинский район Удмуртской Республики (yandex) Москва Широта 55.7558 Долгота 37.6176 (yandex) Широта: 55.727405 Долгота: 52.389287 (yandex) 73 с.ш. 49 в.д (yandex) N 53.3563° E 83.7617° (yandex) 51 ю.ш. и 67 з.д. (yandex) 44° с. ш. 44° в. д (yandex)

43°58’42.70°N, 15°23’0°14E (yandex) Поворино Воронежская область (yandex) N45.24537,E41.83313 (yandex) N 55.3712° E 86.0524° кемерово (yandex) Широта 56.725862. Долгота 60.173889 (yandex) 13 ю.ш 131 в.д (yandex) N44.92851 E38.90888 (yandex) Академика Сатпаева, д. 27 (yandex) Орел 52.990476,36.104598 (yandex) 28 19 45 c.ш. 7 92 ю.д. (yandex)

Орел 52.976441, 36.090167 (yandex) 59.89444,30.26417 (yandex) Широта 55.863518 Долгота 48.800420 (yandex) N53.3563 ‘ E83.7617 (yandex) 41 23 19 N, 2 09 32E (yandex) N56.12321,E43.80339 (yandex) 55°52’13.3 N 37°21’54.6 E (yandex) N45.56579763°, E8.05282006° (yandex) 37.6068 55.7386(latitude,longitude) (yandex) м-5 урал 181.700км Екатеринбург челябинск (yandex)

X 476394.58 Y 2332248.89 (yandex) 41 303921 и 81 901693 (yandex) 59 56 19 с.ш. 30 18 50 в.д (yandex) 51°16’31.2 N 30°13’05.2 E (yandex) N54° 764543 ‘ E48° 713908 ‘ (yandex) N 56.8378° E 60.5968° (yandex) Широта 55,7527 Долгота 37,6172 (yandex) X 488209.26 Y 313590.09 (yandex) новосибирская область, г. Бердск, ул. Зеленая роща, 6 (yandex) мск 66 (yandex)

Определение географических координат объекта по карте.

GoogleYandex

Ссылка на это место:

Twittear

ВконтактеFacebook ()

Градусная сеть: географическая широта

Определить географическую широту – это значит показать расстояние от экватора по меридиану до заданной точки; измеряется она в градусах, от 0° до 90°, бывает северной и южной.

Для того, чтобы узнать широту заданной точки, нужно найти параллель, на которой она расположена. Отсчёт начинается от экватора, следуя строго вдоль меридиана на север или на юг. Расстояние от экватора по меридиану до полюса составляет 90°, чем больше мы будем удаляться от экватора, тем больше будет длина меридиана до нужной нам параллели, тем больше будет её широта.

Некоторые параллели специально подписывают и обозначают на картах. Это тропики и полярные круги. Северный тропик ещё называют Тропиком Рака, а южный – тропиком Козерога. Задание: определите широту каждой из этих условных линий.

Алгоритм определения широты объекта, расположенного на обозначенной на карте параллели:

• Найти объект на карте.
• Найти экватор.
• Определить, в каком направлении нужно двигаться к определяемому объекту – на север или на юг (так мы узнаём, какой будет широта северной или южной).
• Определяем широту параллели, на которой расположен объект. Например, Санкт-Петербург расположен на параллели, отстоящей от экватора на 60° к северу от экватора, значит его широта 60° северной широты (с. ш.).

Если объект расположен между параллелями:

• Определить широту ближайшей к объекту параллели со стороны экватора (действуя по алгоритму, описанному выше).
• Определить количество градусов от этой параллели до нужного нам объекта. Делать это нужно при помощи линейки. Расстояние между соседними параллелями на карте равно 10°, значит 1° — это 1/10 часть этого расстояния.
• Прибавить полученное число к широте найденной ближайшей параллели. (Например, ближайшая к Москве параллель со стороны экватора – 50° с.ш. Расстояние от этой параллели до Москвы равно 6°. Широта Москвы равна 56°, так как если мы к 50 +6 получится именно столько).

А теперь покажите на карте место катастрофы корабля, если в сообщении сказано, что оно произошло на 12 параллели. Чего нам не хватает для точного нахождения места? Данных о долготе.

Знакомство с географической картой

Чтобы понять, как определить географическую широту и долготу на карте, необходимо сначала с ней ознакомиться. В частности, нужно разобраться, как представляются на ней координаты долготы и широты. Во-первых, верхняя часть карты показывает северное полушарие, нижняя часть — южное. Числа, которые находятся слева и справа на краю карты обозначают широту, а числа, расположенные в верхней и в нижней частях карты — это координаты долготы.

Перед тем как определить координаты широты и долготы, необходимо помнить, они на карте представлены в градусах, минутах и секундах. Не следует путать эту систему единиц с десятичными долями градуса. Например, 15′ = 0,25°, 30′ = 0,5°, 45» = 0,75′.

Какова максимальная длина широты и долготы?

Допустимый диапазон широты в градусах составляет -90 и +90 для южного и северного полушария соответственно. Долгота находится в диапазоне -180 и +180, указывая координаты к западу и востоку от меридиана, соответственно.

Для справки: экватор Equator имеет широту 0 °, северный полюс North pole имеет широту 90 ° северной широты (написано 90 ° с.ш. или +90 °) и Южный полюс имеет широту -90 °.

Первичный меридиан Prime Meridian имеет долготу 0 °, которая проходит через Гринвич, Англия. Международная линия дат (IDL) примерно следует 180 ° долготы. Долгота с положительным значением падает в восточном полушарии, а отрицательное значение падает в западном полушарии.

Точность десятичных градусов

Точность в шести (6) десятичных разрядах в координатах с использованием записи в десятичных градусах составляет 10 см (или 0,1 метра). Каждая разница в .000001 в десятичном градусе составляет примерно 10 см в длину. Например, изображения Google Earth и Google Maps обычно имеют разрешение 1 метр, а в некоторых местах разрешение выше 1 дюйма на пиксель. Разрешение в один метр может быть представлено с использованием 5 десятичных знаков, так что более 6 десятичных знаков не имеют значения для этого разрешения. Расстояние между долготами на экваторе такое же, как и широта, но расстояние между долготами достигает нулей на полюсах, когда линии меридиана сходятся в этой точке.

Если значение широты указано как -6.3572375290155 или -6 3.572375290155, вы можете округлить и сохранить до 6 десятичных знаков с точностью 10 см (или 0,1 метра).

Для точности в миллиметрах (мм) представьте широту/долготу с 8 десятичными разрядами в формате десятичных градусов. Поскольку большинству приложений такой уровень точности не нужен, для большинства случаев достаточно 6 десятичных знаков.

В другом направлении целые десятичные градусы представляют расстояние ~ 111 км (или 60 морских миль), а разница в 0,1 десятичного градуса представляет площадь ~ 11 кв. Км.

Вот таблица разницы в # десятичных разрядов по широте с дельта-градусами и расчетным расстоянием в метрах с использованием 0,0 в качестве начальной точки.

Представление градусов-минут-секунд (DMS)

Для обозначения DMS 1 секунда дуги = 1/60/60 градусов = длина ~ 30 метров, а дельта 0,1 секунды составляет ~ 3 метра.

Пример:

• 0 ° 0 ‘0″ W, 0 ° 0’ 0″ N → 0 ° 0 ‘0″ W, 0 ° 0’ 1″ N => 30,715 метров
• 0 ° 0 ‘0″ W, 0 ° 0’ 0″ N → 0 ° 0 ‘0″ W, 0 ° 0’ 0.1″ N => 3.0715 метров

1 минута дуги = 1/60 градуса = ~ 2000 м (2 км)

ОБНОВИТЬ: Вот забавный пост в блоге о точности координат.

Как установить географические координаты на карте?

Для расчета координат объекта на карте необходимо сначала определить, в каком из полушарий он находится. Далее следует выяснить, между какими параллелями располагается нужная точка, и установить точное число градусов – обычно они прописываются по бокам географической карты. После этого можно переходить к определению долготы, установив сначала, в каком из полушарий расположен объект относительно Гринвича. Определение градусов долготы осуществляется аналогично широте. Если нужно выяснить расположение точки в трехмерном пространстве, дополнительно используется ее высота относительно уровня моря.