Онлайн расчет расстояния по координатам + формула

Другие методы прокладки маршрута

Пожалуй, самая простая альтернатива — это открыть атлас автодорог и на глаз проложить маршрут по карте.
Затем, прокатив по маршруту курвиметр, можно получить приблизительный километраж.
Оценить время поездки будет сложнее: для этого придется разбить маршрут на фрагменты с одинаковым классом дорог и
измерить сумму длин фрагментов каждого класса.
Далее, зная среднюю скорость для каждого класса дорог, нетрудно рассчитать время, поделив путь на скорость.

Если курвиметра нет под рукой, то можно воспользоваться линейкой.
Приложите нулевую отметку линейки к начальному пункту маршрута и двигайте линейку, плотно примыкая ее к извилинам
дороги.

Рассчитать расстояние между городами также можно с помощью таблиц, которые опубликованы в атласах и
справочниках.
Это достаточно удобно для маршрутов, начинающихся и заканчивающихся в крупных городах.
Мелких населенных пунктов, как правило, нет в таблицах.

Меридиан

Меридианом в географии называют половину линии сечения земной поверхности, проведённой через земную ось вращения и любую точку на поверхности. Все воображаемые меридианы, которых может быть бесконечное количество, соединяются на полюсах — Северном и Южном. Протяжённость каждого из них — 20 004 276 метров.

Хотя меридианов мысленно можно провести как угодно много, для удобства передвижения, составления карт их количество, расположение упорядочили международными договорами. В 1884 году на Международной меридианной конференции в Вашингтоне постановили, что начальным меридианом (нулевым) станет тот, что проходит через Гринвич — округ на юго-востоке Лондона.

Однако не все сразу согласились с таким решением. Например, в России даже после 1884 года вплоть до начала ХХ века нулевым меридианом считали собственный — Пулковский: он «проходит» через Круглый зал Пулковской обсерватории.

Масштаб. Измерение расстояний по планам, картам и глобусу. Урок 3

Чтобы измерить расстояние по плану, карте или глобусу, нужно знать, что такое масштаб и уметь им пользоваться. Масштаб – одна из основных математических составляющих любой географической модели Земли, он показывает, во сколько раз уменьшены все расстояния на карте по сравнению с теми же расстояниями на местности.

Если масштабирование не произвести, то никакой бумаги не хватит, чтобы изобразить на ней даже небольшой участок поверхности. На старинных картах размеры и расстояния уменьшены в неодинаковое количество раз, поэтому по ним можно узнать очертания объектов, но не их величину.

Как определить протяженность

В курсе географии учащимся нередко предлагается определить протяженность материка с юга на север или с запада на восток. На практике с подобной задачей сталкиваются, например, архитекторы. Аналогичная методика расчетов применяется и в космических исследованиях. Для выполнения таких заданий необходимо знать соотношение между градусами сетки координат и количеством километров, характерное для каждого конкретного объекта во Вселенной.

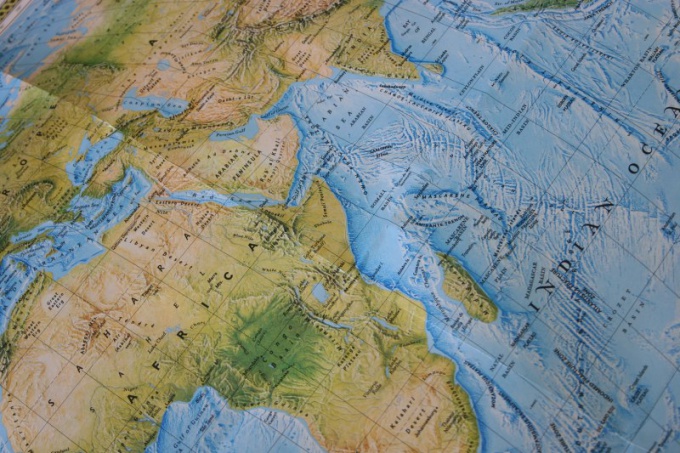
Протяженность материка — это расстояние между его крайними точками. Северные, южные, западные и восточные оконечности известны, их можно найти в географических справочниках и энциклопедиях. Например, самая южная точка Африки — мыс Игольный, а самая западная материковая точка Евразии — мыс Рока

Обратите внимание на то, что протяженность материка обычно определяется по континентальным крайним точкам. Но в задании может быть предложено также найти расстояние между крайними островными точками

Найти крайние точки можно и на географической карте, бумажной или электронной. Северная оконечность — самая выпуклая верхняя точка материка. Внизу, соответственно, будет находиться самая южная. Определите их широту. Если под рукой нет никакого справочника, посмотрите, на каких параллелях находятся оба необходимых вам пункта. Найдите разность между показателями этих параллелей. Это и будет протяженность материка с севера на юг, выраженная в градусах. Не забудьте, что части одного и того же материка могут располагаться в северном и южном полушариях. В этом случае значения широты суммируются. То есть если вам, например, нужно определить расстояние между точками 45° и 75° северной широты, то оно будет равно 30°. Если же одна точка находится на 45° северной, а вторая — на 75° южной широты, то расстояние между ними составит 120°.

Определите протяженность материка с севера на юг в километрах. Посмотрев на карту, вы увидите, что все меридианы равны, поэтому и количество километров в одном градусе тоже будет одинаковым. Оно составляет приблизительно 111 км. Умножив это число на количество градусов, вы получите протяженность в километрах.

Протяженность с запада на восток в градусах определяется точно таким же образом, что и с севера на юг. Найдите крайние точки. Определите их координаты — в данном случае вам важна долгота, то есть меридиан, проходящий через каждый из этих пунктов. Вычислите количество градусов.

Чтобы найти протяженность с запада на восток в километрах, необходимо знать косинус угла, соответствующий показателю данной параллели. Его умножают на величину градуса экватора. Он составляет примерно 111 км. Для более точных вычислений используют немного другой показатель — 111,3 км.

Источник

Определить координаты точки по карте — ? с видео

Чтобы вычислить географические координаты объекта, нужно:

1. Определить его географическую широту
2. Определить его географическую долготу.
3. Совместить широту с долготой.

Для того, чтобы определить координаты менее масштабных объектов, нужна подробная карта, где можно оперировать не только градусами, но и минутами с секундами. Детализация координат до географических секунд конкретизирует местоположение объекта с точностью до 30 метров.

В углу карты обычно есть масштабная линейка, где указано соотношение расстояний на карте к расстояниям в географических координатах и километрах.

Тогда приложением обыкновенной миллиметровой линейки к масштабной можно выяснить, что, к примеру, 1 ° широты равен 30 мм, 1 ° долготы — 40 мм. Далее при помощи простых измерений на карте и математических пропорций легко вычислить точные координаты.

Если вычисления потребуются в походе, лучше заранее потренироваться дома.

Видео-пример определения координат на топографической карте

https://youtube.com/watch?v=5TnoF_S5qeA

Как записывается и читается тысячная

Тысячные записываются и читаются соответственно так:

• одна тысячная — 0,01 — ноль, ноль один
• шесть тысячных — 0,06 — ноль, ноль шесть
• 25 тысячных — 0,25 — ноль, двадцать пять
• 130 тысячных- 1,30 — один, тридцать
• 1500 тысячных — 15,00 — пятнадцать, ноль ноль

Как производится измерение тысячных

Определение угла по приборам. Измерение углов в тысячных может производиться угломерным кругом артиллерийской буссоли, сеткой бинокля и перископа, шкалой боковых поправок и лимбами маховика снайперского прицела, а также подручными предметами.

Буссоль имеет шкалу на круге, разделенную на большие деления в 1-00 и малые в 0-20.
Бинокль и перископ имеют сетки, разделенные на большие деления в 0-10 (десять тысячных) и малые в 0,05 (пять тысячных).
Прицелы пулеметные и снайперские имеют деления в 0,01 (одну тысячную). Пример: Определение дистанции или размеров объекта с помощью прицела ПСО-1

Глазомерное определение угла заключается в сопоставлении измеряемого угла с известным. Углы определенной величины можно получить следующими способами. Прямой угол получается между направлением рук, одна из которых вытянута вдоль плеч, а другая — прямо перед собой. От составленного таким приемом угла можно отложить какую-то часть его, имея в виду, что 1/2 часть соответствует углу 7-50 (45°), 1/3 — углу 5-00 (30°) и т.д. Угол 2-50 (15°) получается путем визирования через большой и указательный пальцы, расставленные под углом 90° и удаленные на 60 см от глаза, а угол 1-00 (6°) соответствует углу визирования на три сомкнутых пальца: указательный, средний и безымянный.

Угловые величины между пальцами руки

Определение угла по циферблату часов. Часы держат перед собой горизонтально и поворачивают их так, чтобы штрих, соответствующий 12 часам на циферблате, совместился с направлением левой стороны угла. Не меняя положения часов, замечают пересечение направления правой стороны угла с циферблатом и отсчитывают количество минут. Это и будет величина угла в больших делениях угломера. Например, отсчет 25 минут соответствует 25-00.

Определение угла компасом. Визирное приспособление компаса предварительно совмещают с начальным штрихом лимба, а затем визируют по направлению левой стороны измеряемого угла и, не меняя положения компаса, против направления правой стороны угла снимают отсчет по лимбу. Это и будет величина измеряемого угла или его дополнение до 360° (60-00), если подписи на лимбе идут против хода часовой стрелки.
Величину угла компасом можно определить более точно, измерив азимуты направлений сторон угла. Разность азимутов правой и левой сторон угла будет соответствовать величине угла. Если разность получится отрицательной, то необходимо прибавить 360° (60-00). Средняя ошибка определения угла этим способом составляет 3-4°.

С помощью линейки. Если линейку держать на расстоянии 50 см от глаз, то деление в 1 мм будет соответствовать 0-02. При удалении линейки от глаз на 60 см 1 мм соответствует 6′, а 1 см — 1°. Для измерения угла в тысячных линейку держат перед собой на расстоянии 50 см от глаз и подсчитывают число миллиметров между предметами, обозначающими направления сторон угла. Полученное число умножают на 0-02 и получают величину угла в тысячных. Для измерения угла в градусах порядок действий тот же, только линейку необходимо держать на расстоянии 60 см от глаз.
Точность измерения углов с помощью линейки зависит от умения выносить линейку точно на 50 или на 60 см от глаз. В этой связи можно рекомендовать следующее: к артиллерийскому компасу привязывается шнурок такой длины, чтобы линейка компаса, повешенного на шею и отнесенного вперед на уровень глаза наблюдателя, оказывалась от него на расстоянии ровно 50 см.

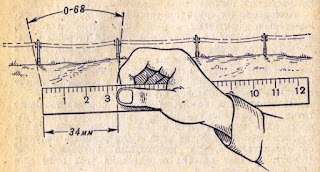Измерение угла линейкой, удаленной на 50 см от глаза наблюдателя

Формула тысячной

Формула, показывающая взаимосвязь дальности до цели, высоты (длины) цели и ее угловой величины называется формулой тысячной и применяется не только в артиллерии, но и в военной топографии: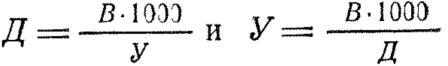

где:

Д — дальность до предмета в метрах

У — угол, под которым виден предмет в тысячных

В — высота (ширина) предмета в метрах

В получившемся результате может быть погрешность в 5 %, что можно игнорировать для большинства практических расчётов.

Есть правило для лучшего запоминания соотношения: «предмет, линейным размером 1 метр, удалённый от наблюдателя на 1 километр, виден под угловой величиной в 1 тысячную».

Как измерить расстояние на карте с помощью градусной сетки?

Определение местоположения на карте. Изображение: https://studopedia.org

С помощью карты можно определять расстояние между точками на земной поверхности, но точность таких вычислений невысока.

Ситуация относительно проста, если точки лежат на одном меридиане. Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.

111,3х(50° – 32°) = 111,3х16 = 1780,8 км

Ситуация меняется, когда одна точка имеет северную, а другая – южную широту. В этом случае широты уже надо складывать. Так, если бы точка Б из предыдущего примера располагалась бы на южной широте 32°, то расстояние от А до Б составило бы:

111,3х(50° + 32°) = 111,3х82 = 9126,6 км

Ситуация усложняется, когда точки находятся на разных меридианах, но на одной параллели. Если у обеих точек долгота западная (или, наоборот, восточная), то сначала надо найти разницу их долгот. Если же одна точка имеет восточную, а другая западную долготу, то их надо суммировать. Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:

Широта параллели	Длина ее дуги величиной в 1°
0°	111,3
5°	110,9
10°	109,6
15°	107,6
20°	104,6
25°	102,1
30°	96,5
35°	91,3
40°	85,4
45°	78,8
50°	71,7
55°	64,0
60°	55,8
65°	47,2
70°	38,2
75°	28,9
80°	19,4
85°	9,7
90°

Например, нужно найти расстояние между точками, имеющими координаты:

А – 60° с. ш, 39° з. д.Б – 60° с. ш, 25° з. д.

Широты у них одинаковы, поэтому смотрим на долготу. Она у обеих точек западная, поэтому надо найти их разницу:

39° – 25° = 14°

Полученный результат надо умножить на длину 1° параллели, широта которой составляет 60°. По табличке определяем, что на широте 60° дуга в 1° имеет длину 55,8 км. Перемножаем два числа:

14°х 55,8 км = 781,2 км

Список использованных источников

Источник

Формулы плоской поверхности

Планарное приближение для поверхности Земли может быть полезно на небольших расстояниях. Точность вычислений расстояний с использованием этого приближения становится все более неточной, так как:

• Расстояние между точками становится больше;
• Точка становится ближе к географическому полюсу.

Кратчайшее расстояние между двумя точками на плоскости — прямая. Теорема Пифагора используется для вычисления расстояния между точками на плоскости.

Даже на небольших расстояниях точность вычислений географических расстояний, предполагающих наличие плоской Земли, зависит от метода, с помощью которого координаты широты и долготы проецируются на плоскость. Проекция координат широты и долготы на плоскость — это область картографии .

Формулы, представленные в этом разделе, обеспечивают разную степень точности.

Сферическая Земля в проекции на самолет

Эта формула учитывает изменение расстояния между меридианами в зависимости от широты:

D знак равно р ( Δ ϕ ) 2 + ( потому что ⁡ ( ϕ м ) Δ λ ) 2 , {\ displaystyle D = R {\ sqrt {(\ Delta \ phi) ^ {2} + (\ cos (\ phi _ {m}) \ Delta \ lambda) ^ {2}}},}

где:

Δ ϕ {\ displaystyle \ Delta \ phi \, \!} и указаны в радианах; Δ λ {\ displaystyle \ Delta \ lambda \, \!}

ϕ м {\ Displaystyle \ phi _ {м} \, \!} должны быть в единицах, совместимых с методом, используемым для определения потому что ⁡ ( ϕ м ) . {\ Displaystyle \ соз (\ фи _ {м}). \, \!}

Чтобы преобразовать широту или долготу в радианы, используйте

1 ∘ знак равно ( π 180 ) р а d я а п s . {\ displaystyle 1 ^ {\ circ} = (\ pi / 180) \, \ mathrm {радианы}.}

Это приближение очень быстрое и дает довольно точный результат для небольших расстояний. Кроме того, при упорядочивании местоположений по расстоянию, например, в запросе к базе данных, быстрее выполняется сортировка по квадрату расстояния, что устраняет необходимость в вычислении квадратного корня.

Эллипсоидальная Земля в проекции на плоскость

FCC предусматривает следующие формулы для расстояний , не превышающих 475 километров (295 миль):

D знак равно ( K 1 Δ ϕ ) 2 + ( K 2 Δ λ ) 2 , {\ displaystyle D = {\ sqrt {(K_ {1} \ Delta \ phi) ^ {2} + (K_ {2} \ Delta \ lambda) ^ {2}}},}

где

D {\ Displaystyle D \, \!} = Расстояние в километрах;

Δ ϕ {\ displaystyle \ Delta \ phi \, \!} и находятся в градусах; Δ λ {\ displaystyle \ Delta \ lambda \, \!}

ϕ м {\ Displaystyle \ phi _ {м} \, \!} должны быть в единицах, совместимых с методом, используемым для определения потому что ⁡ ( ϕ м ) ; {\ Displaystyle \ соз (\ фи _ {м}); \, \!}

K 1 знак равно 111,13209 — 0,56605 потому что ⁡ ( 2 ϕ м ) + 0,00120 потому что ⁡ ( 4 ϕ м ) ; K 2 знак равно 111,41513 потому что ⁡ ( ϕ м ) — 0,09455 потому что ⁡ ( 3 ϕ м ) + 0,00012 потому что ⁡ ( 5 ϕ м ) . {\ displaystyle {\ begin {align} K_ {1} & = 111.13209-0.56605 \ cos (2 \ phi _ {m}) + 0,00120 \ cos (4 \ phi _ {m}); \\ K_ {2} & = 111,41513 \ cos (\ phi _ {m}) — 0,09455 \ cos (3 \ phi _ {m}) + 0,00012 \ cos (5 \ phi _ {m}). \ End {align}} \, \!}

Где и выражены в километрах на градус. Интересно отметить, что:
K 1 {\ displaystyle K_ {1}} K 2 {\ displaystyle K_ {2}}

K 1 знак равно M π 180 {\ displaystyle K_ {1} = M {\ frac {\ pi} {180}} \, \!} = километров на градус разницы широты;

K 2 знак равно потому что ⁡ ( ϕ м ) N π 180 {\ displaystyle K_ {2} = \ cos (\ phi _ {m}) N {\ frac {\ pi} {180}} \, \!} = километров на градус разницы долготы;

где и являются м eridional и его перпендикулярен, или « п НПУ », (выражения в формуле FCC являются производными от биномиальной серии формы расширения и , набора к Кларку 1866 г. эллипсоиду ). M {\ Displaystyle M \, \!} N {\ Displaystyle N \, \!} M {\ Displaystyle M \, \!} N {\ Displaystyle N \, \!}

Для более эффективной с вычислительной точки зрения реализации вышеприведенной формулы несколько приложений косинуса можно заменить одним приложением и использованием рекуррентного соотношения для полиномов Чебышева .

Формула плоской Земли в полярных координатах

D знак равно р θ 1 2 + θ 2 2 — 2 θ 1 θ 2 потому что ⁡ ( Δ λ ) , {\ displaystyle D = R {\ sqrt {\ theta _ {1} ^ {2} \; {\ boldsymbol {+}} \; \ theta _ {2} ^ {2} \; \ mathbf {-} \; 2 \ theta _ {1} \ theta _ {2} \ cos (\ Delta \ lambda)}},}

где значения ширины в радианах. Для широты, измеряемой в градусах, широта в радианах может быть вычислена следующим образом: θ знак равно π 180 ( 90 ∘ — ϕ ) . {\ displaystyle \ theta = {\ frac {\ pi} {180}} (90 ^ {\ circ} — \ phi). \, \!}

Определяем географические координаты

Градусная сеть поможет определить географические координаты. Поскольку мы имеем дело с дугами и окружностями, то все расчеты координат следует производить в градусах, минутах и секундах. Поэтому и сеть называется градусной.

Градусная сеть позволяет определять местоположение любой точки на земной поверхности с помощью географических координат – широты и долготы. При определении географических координат Земля принимается за шар, хотя мы помним, что она геоид.

Географическая широта φ – угол между плоскостью экватора и отвесной линией в данной точке, другими словами – это угловое расстояние точки от экватора по меридиану. Измеряется от 0 (экватор) до 90° (полюса). Различают северную (лежащую в Северном полушарии) и южную (расположенную в Южном полушарии) широту. Северную широту принято считать положительной, а южную – отрицательной. О широтах, близких к экватору, принято говорить как о низких, к полюсам – как о высоких.

Все точки, лежащие на одной параллели, имеют одинаковую широту. На глобусе параллели подписываются на 0° и 180° меридианах, на картах – на боковых рамках.

Лучшие статьи : Ночные животные — характеристика, происхождение, адаптации и примеры

Определение географической широты

Все параллели – окружности, они содержат 360°. От экватора до каждого из полюсов градусное расстояние составляет 90°.

Ответьте на вопросы. По какой параллели можно быстрее совершить кругосветное путешествие – по 0° или по 66°? Почему кругосветные плавания нельзя считать доказательством шарообразности Земли?

«… 7июня 1862 г. трёхмачтовое судно «Британия» … Глазго потерпело крушение …гони … южн… берег… два матроса Капитан Гр… дости… контин… пл… жесток… инд… брошен этот документ … долготы и 37° … широты. Окажите им помощь… погибнут …» — это всё, что было известно о гибели судна капитана Гранта из романа Жюля Верна «Дети капитана Гранта». Но одной широты недостаточно, чтобы определить положение объекта на Земле. Ведь 37 параллель только в Южном полушарии пересекает и Южную Америку, и Австралию, и Новую Зеландию, и многочисленные острова.

Географическая долгота λ – двугранный угол, образованный плоскостью начального меридиана и плоскостью меридиана, проходящего через данную точку, иначе – угловое расстояние точки от начального меридиана.

Все меридианы – дуги и по длине они одинаковые. Поэтому люди договорились, от какого из них вести отсчёт. Долгое время каждая страна вела счёт долготы от своего начального меридиана, Франция – от Парижского, Россия – от Пулковского (с обсерваторией) у Санкт-Петербурга, США и Англия – от Гринвичского. С 1884 года нулевым и начальным меридианом для всех стран считается Гринвичский. Он проходит через пригород города Лондона Гринвич, где в 1637 г была основана одна из старейших в мире астрономических обсерваторий. Выбор начального меридиана очень важен, так как с ним связан и отсчёт времени.

От нулевого меридиана ведут счёт расстояния в градусах на восток от 0° до 180° и на запад 0° до 180°. Нулевой меридиан, продолжением которого является 180°, делит Землю на Западное и Восточное полушария. Меридианы показывают направление север-юг.

К востоку от Гринвичского меридиана долгота восточная, к западу – западная. От неё зависит местное солнечное время. Все точки, лежащие на одном меридиане, имеют одинаковую долготу. На глобусе меридианы подписываются на экваторе, на картах – на экваторе или на верхней и нижней рамках. На практике географическую долготу определяют по разнице местного времени между нулевым меридианом и меридианом пункта наблюдения.

Определение географической долготы

Любая точка на земле имеет свой «географический адрес». Теперь мы знаем, что этот адрес состоит из двух частей. Это как при игре в «морской бой», где тоже используется адрес. Две части географического адреса – широта и долгота, определить их нам помогает градусная сеть. Широта – место точки на определённой параллели, долгота – на меридиане. Место их пересечения и есть географический адрес – географические координаты.

Зная географические координаты можно найти любой объект на карте. И, наоборот, можно нанести новый объект на карту, определив его географические координаты, как это делали все первооткрыватели. Ошибки в этом стоили многих жизней.

До времени существования навигаторов, географические координаты в открытом море определяли сначала с помощью такого прибора, как астролябия, а затем его заменил секстант.

АстролябияСекстант

Тысячная, формулы тысячной для определения расстояний и дальности, простейшие способы измерения углов на местности с помощью тысячных.

В войсковой практике, где при вычислениях постоянно приходится пользоваться соотношениями между угловыми и линейными величинами, вместо градусной системы мер применяется артиллерийская (линейная). Более простая и удобная для быстрых приближенных вычислений. За единицу угловых мер артиллеристы принимают центральный угол круга, стянутого дугой, равной 1/6000 длины окружности.

Этот угол называется делением угломера. Так как используется во всех артиллерийских угломерных приборах. Иногда этот угол называют — тысячная. Это название объясняется тем, что длина дуги такого угла по окружности равна приближенно тысячной доле ее радиуса

Это очень важное обстоятельство

Следовательно, при наблюдении окружающих нас объектов, мы находимся как бы в центре концентрических окружностей, радиусы которых равны расстояниям до объектов. И мерой центральных углов будут служить линейные отрезки. Равные тысячной доле расстояния до объектов. Так, если дом длиной 5 метров расположен на удалении от наблюдателя на 1000 метров, то он укладывается в центральный угол, равный пяти тысячным. Такой угол записывается на бумаге так : 0-05, и читается — ноль, ноль пять.

Если длина забора равна 100 метрам, то он укладывается в центральный угол, равный 100 тысячным, одно большое деление угломерного прибора. Записывается этот угол на бумаге так : 1-00 тысячная, и читается — один, ноль. Из этих примеров видно, что углы позволяют очень быстро и легко посредством простейших арифметических действий переходить из угловых измерений к линейным и обратно.

Так, например, если рядом с домом, находящимся от наблюдателя на расстоянии Д-1500 метров (Д — дальность) находится дерево и угол между ними укладывается в пятьдесят пять тысячных — У=0-55 (У — угол) и требуется определить расстояние от дома до дерева — В (В — расстояние), то из пропорции В : Д = У : 1000 вытекает формула для определения линейных размеров.

Д = 1000 х В / У

Решим простой пример определения расстояния через формулу тысячной — у столба высотой 6 метров вы видите человека. Требуется определить расстояние до него. Вначале определяем, в какой угол укладывается высота столба. Допустим, что высота столба укладывается в угол У=0—05 (пять тысячных). Тогда по формуле для определения дальности получим : Д = 1000 х 6 / 5 = 1200 метров.

Использование двух вышеприведенных формул позволяет определять быстро и точно любые линейные и угловые величины на местности.

Между делениями угломера (в тысячных) и обычной градусной системой угловых мер существуют соотношения. Одна тысячная 0-01 равна 3,6″ (минуты), а большое деление угломера (1-00) = 6 градусов. Эти соотношения позволяют при необходимости осуществлять переход от одной системы измерений к другой.

Простейшие способы измерения углов на местности с помощью тысячных.

Углы на местности можно измерять с помощью полевого бинокля, линейки и подручных предметов. В поле зрения бинокля имеются две взаимно-перпендикулярные угломерные шкалы для измерения горизонтальных и вертикальных углов. Величина одного большого деления этих шкал соответствует 0-10, а малого 0-05 тысячных.

Для измерения угла между двумя направлениями надо, глядя в бинокль, совместить какой-либо штрих угломерной шкалы с одним из этих направлений и подсчитать число делений до второго направления. Так, например, отдельное дерево (пулемет противника) расположено влево от дороги на угол 0-30.

Вертикальной шкалой пользуются при определении вертикальных углов. В случае их больших размеров можно пользоваться и горизонтальной шкалой. Повернув бинокль вертикально. При отсутствии бинокля углы можно измерять обычной линейкой с миллиметровыми делениями. Если такую линейку держать перед собой на расстоянии 50 см от глаз, то одно ее деление (1 мм) будет соответствовать углу в две тысячных (0-02).

Точность измерения углов таким способом зависит от навыка в вынесении линейки точно на 50 см от глаза. Этого можно достигнуть, привязав к линейке нитку и закусив ее зубами на расстоянии 50 см. С помощью линейки можно измерять углы и в градусах. В этом случае ее следует выносить на расстояние 60 см от глаза. Тогда 1 см на линейке будет соответствовать углу в 1 градус.

При отсутствии линейки с делениями можно использовать пальцы, ладонь или любой небольшой предмет (спичечную коробку, карандаш). Размер которых в миллиметрах, а следовательно, и в тысячных известен. Такая мерка выносится на расстояние 50 см от глаза и по ней путем сравнения определяется искомая величина угла.

По материалам книги «Карта и компас — мои друзья». Клименко А.И.

Градусная сеть, ее элементы. Географические координаты — Гипермаркет знаний

Гипермаркет знаний>>География>>География 6 класс>> Градусная сеть, ее элементы. Географические координаты

§ 3. Градусная сеть, ее элементы. Географические координаты

Ориентироваться по карте и находить точное местоположение географических объектов на поверхности Земли позволяет градусная сеть, или система линий параллелей и меридианов.

Параллели (от греч. parallelos — букв, идущий рядом) — это линии, условно проведенные на поверхности Земли параллельно экватору. Параллелей на карте и глобусе можно провести сколько угодно, но обычно на учебных картах их проводят с интервалом 10—20°. Параллели всегда ориентированы с запада на восток. Длина окружности параллелей уменьшается от экватора к полюсам.

Экватор (от лат. aequator — уравнитель) — воображаемая линия на земной поверхности, полученная при мысленном рассечении Земного шара плоскостью, проходящей через центр Земли перпендикулярно оси ее вращения. Все точки на экваторе оказываются равноудаленными от полюсов. Экватор делит Земной шар на два полушария — Северное и Южное.

Меридиан (от лат. meridians — полуденный) — кратчайшая линия, условно проведенная поверхности Земли от одного полюса до другого.Таблица 2

                          Сравнительная характеристика меридианов и параллелей

Признаки	Меридианы	Параллели
Направление	С.-Ю.	З.-В.
Название нулевой линии	Гринвичский (Лондонский) меридиан	Экватор
Длина, км	20 000	От 40 000 до 0
Длина одного градуса, км	111	От 111 до 0
Форма на глобусе	Полуокружность	Окружности
Форма на карте полушарий	Срединные меридианы — прямые, остальные — дуги	Экватор — прямая, остальные — дуги

Географические полюсы (от лат. polus — ось) — математически высчитанные точки пересечения воображаемой оси вращения Земли с земной поверхностью. Меридианы можно провести через любые точки на земной поверхности, и все они будут проходить через оба полюса Земли.

Меридианы ориентированы с севера на юг, и все имеют одинаковую длину (от полюса до полюса) — около 20000 км. Средняя длина 1° меридиана: 20004 км : 180° = 111 км. Направление местного меридиана в любой точке можно определить в полдень по тени от любого предмета.

В Северном полушарии конец тени всегда показывает направление на север, в Южном полушарии — на юг.

Градусная, или картографическая, сеть служит для определения географических координат точек земной поверхности — долгот и широт — или нанесения на карту объектов по их координатам. Все точки данного меридиана имеют одну и ту же долготу, а все точки параллели — одинаковую широту. 

Географическая широта — это величина дуги меридиана в градусах от экватора до заданной точки. Так, Санкт-Петербург находится в Северном полушарии, на 60° северной широты (сокращенно с.ш.

), Суэцкий канал — на 30° с.ш. Определить географическую широту любой точки на глобусе или карте — это определить, на какой параллели она находится.

К югу от экватора любая точка будет иметь южную широту (сокращенно ю. ш.).

Географическая долгота — это величина дуги параллели в градусах от начального меридиана до заданной точки. Начальный, или нулевой, меридиан выбран условно и проходит через Гринвичскую обсерваторию, находящуюся недалеко от Лондона. К востоку от этого меридиана определяется восточная долгота (в. д.), к западу — западная (з.д.) (рис. 10).

Широта и долгота любой точки Земли составляют ее графические координаты. Так, географические координаты Москвы — 56° с.ш. и 38° в. д.

Максаковский В.П., Петрова Н.Н., Физическая и экономическая география мира. — М.:Айрис-пресс, 2010. — 368с.:ил.

Видеопо географии скачать, домашнее задание, учителям и школьникам на помощь онлайн

Содержание урока конспект урока
опорный каркас презентация урока
акселеративные методы интерактивные технологии Практика
задачи и упражнения самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа
фотографии, картинки графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения рефераты
статьи фишки для любознательных шпаргалки учебники основные и дополнительные
словарь терминов прочие
Совершенствование учебников и уроков исправление ошибок в учебнике
обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки
календарный план на год методические рекомендации программы
обсуждения Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.