Расчет расстояний между городами по их координатам

Примеры задач с решением

Задача 1

Дан куб \(ABCDA_1B_1C_1D_1\) с ребром равным \(\sqrt{32}\) см. Найти расстояние между прямыми \(DB_1\) и \(CC_1\).

Решение

Расстояние между скрещивающимися прямыми будем искать в качестве расстояния между прямой \(CC_1\) и плоскостью, проходящей через \(DB_1\) параллельно \(CC_1\). Так как \(DD_1\parallel CC_1\), плоскость \((B_1D_1D)\) параллельна \(СС_1\).

Сначала нужно доказать, что \(CO\) — перпендикуляр, проведенный к этой плоскости. \(CO\perp BD\) (как диагонали квадрата) и \(CO\perp DD_1\) (так как ребро \(DD_1\) перпендикулярно всей плоскости \((ABC)\)). Получается, \(CO\) перпендикулярен двум пересекающимся прямым из плоскости. Значит, \(CO\perp(B_1D_1D)\).

\(AC\) — диагонально квадрата — равна \(AB\sqrt2\), то есть \(AC=\sqrt{32}\times\sqrt2=\sqrt{64}=8\) см. Следовательно, \(CO=\frac12\times AC=4\) см.

Ответ: 4 см.

Задача 2

В трехмерном пространстве в прямоугольной системе координат Oxyz заданы две скрещивающиеся прямые a и b. Прямую a определяют параметрические уравнения прямой в пространстве:

\(\left\{\begin{array}{l}x=-2\\y=1+2\times\lambda\\z=4-3\times\lambda\end{array}\right.\)

А прямую b канонические уравнения прямой в пространстве:

\(\frac x1=\frac{y-1}{-2}=\frac{z+4}6\).

Вычислить расстояние между заданными прямыми.

Решение

Прямая a проходит через точку \(M_1(-2, 1, 4)\) и имеет направляющий вектор \(\overrightarrow a=(0, 2, -3)\). Прямая b проходит через точку \(M_2 (0, 1, -4)\), аее направляющий вектором является вектор \(\overrightarrow b=(1, -2, 6)\).

Найдем векторное произведение векторов\( \overrightarrow a=(0, 2, -3)\) и \(\overrightarrow b=(1, -2, 6): \left=\begin{vmatrix}\overrightarrow i&\overrightarrow j&\overrightarrow k\\0&2&-3\\1&-2&6\end{vmatrix}=6\times\overrightarrow i-3\times\overrightarrow j-2\times\overrightarrow k\).

Так, \(\overrightarrow n=\left\) плоскости X, проходящей через прямую b параллельно прямой a, имеет координаты (6, -3, -2).

Таким образом, уравнение плоскости X есть уравнение плоскости, проходящей через точку \(M_2(0, 1, -4)\) и имеющей нормальный вектор \(\overrightarrow n=(6, -3, -2)\):

\(6\times(x-0)-3\times(y-1)-2\times(z-(-4))=0\;\leftrightarrow6x-3y-2z-5=0\)

Нормирующий множитель для общего уравнения плоскости \(6x-3y-2z-5=0\) равен \\(frac1{\sqrt{6^2+{(-3)}^2+{(-2)}^2}}=\frac17\). Значит, нормальное уравнение этой плоскости выглядит как \(\frac67x-\frac37y-\frac27z-\frac57=0\).

Воспользуемся формулой для вычисления расстояния от точки \(M_1(-2, 1, 4)\) до плоскости \(\frac67x-\frac37y-\frac27z-\frac57=0: \left|M\_1H\_1\right|=\left|\frac67\times(-2)-\frac37\times1-\frac27\times4-\frac57\right|=\left|\frac{-28}7\right|=4\) см.

Формулы плоской поверхности

Планарное приближение для поверхности Земли может быть полезно на небольших расстояниях. Точность вычислений расстояний с использованием этого приближения становится все более неточной, так как:

• Расстояние между точками становится больше;
• Точка становится ближе к географическому полюсу.

Кратчайшее расстояние между двумя точками на плоскости — прямая. Теорема Пифагора используется для вычисления расстояния между точками на плоскости.

Даже на небольших расстояниях точность вычислений географических расстояний, предполагающих наличие плоской Земли, зависит от метода, с помощью которого координаты широты и долготы проецируются на плоскость. Проекция координат широты и долготы на плоскость — это область картографии .

Формулы, представленные в этом разделе, обеспечивают разную степень точности.

Сферическая Земля в проекции на самолет

Эта формула учитывает изменение расстояния между меридианами в зависимости от широты:

D знак равно р ( Δ ϕ ) 2 + ( потому что ⁡ ( ϕ м ) Δ λ ) 2 , {\ displaystyle D = R {\ sqrt {(\ Delta \ phi) ^ {2} + (\ cos (\ phi _ {m}) \ Delta \ lambda) ^ {2}}},}

где:

Δ ϕ {\ displaystyle \ Delta \ phi \, \!} и указаны в радианах; Δ λ {\ displaystyle \ Delta \ lambda \, \!}

ϕ м {\ Displaystyle \ phi _ {м} \, \!} должны быть в единицах, совместимых с методом, используемым для определения потому что ⁡ ( ϕ м ) . {\ Displaystyle \ соз (\ фи _ {м}). \, \!}

Чтобы преобразовать широту или долготу в радианы, используйте

1 ∘ знак равно ( π 180 ) р а d я а п s . {\ displaystyle 1 ^ {\ circ} = (\ pi / 180) \, \ mathrm {радианы}.}

Это приближение очень быстрое и дает довольно точный результат для небольших расстояний. Кроме того, при упорядочивании местоположений по расстоянию, например, в запросе к базе данных, быстрее выполняется сортировка по квадрату расстояния, что устраняет необходимость в вычислении квадратного корня.

Эллипсоидальная Земля в проекции на плоскость

FCC предусматривает следующие формулы для расстояний , не превышающих 475 километров (295 миль):

D знак равно ( K 1 Δ ϕ ) 2 + ( K 2 Δ λ ) 2 , {\ displaystyle D = {\ sqrt {(K_ {1} \ Delta \ phi) ^ {2} + (K_ {2} \ Delta \ lambda) ^ {2}}},}

где

D {\ Displaystyle D \, \!} = Расстояние в километрах;

Δ ϕ {\ displaystyle \ Delta \ phi \, \!} и находятся в градусах; Δ λ {\ displaystyle \ Delta \ lambda \, \!}

ϕ м {\ Displaystyle \ phi _ {м} \, \!} должны быть в единицах, совместимых с методом, используемым для определения потому что ⁡ ( ϕ м ) ; {\ Displaystyle \ соз (\ фи _ {м}); \, \!}

K 1 знак равно 111,13209 — 0,56605 потому что ⁡ ( 2 ϕ м ) + 0,00120 потому что ⁡ ( 4 ϕ м ) ; K 2 знак равно 111,41513 потому что ⁡ ( ϕ м ) — 0,09455 потому что ⁡ ( 3 ϕ м ) + 0,00012 потому что ⁡ ( 5 ϕ м ) . {\ displaystyle {\ begin {align} K_ {1} & = 111.13209-0.56605 \ cos (2 \ phi _ {m}) + 0,00120 \ cos (4 \ phi _ {m}); \\ K_ {2} & = 111,41513 \ cos (\ phi _ {m}) — 0,09455 \ cos (3 \ phi _ {m}) + 0,00012 \ cos (5 \ phi _ {m}). \ End {align}} \, \!}

Где и выражены в километрах на градус. Интересно отметить, что:
K 1 {\ displaystyle K_ {1}} K 2 {\ displaystyle K_ {2}}

K 1 знак равно M π 180 {\ displaystyle K_ {1} = M {\ frac {\ pi} {180}} \, \!} = километров на градус разницы широты;

K 2 знак равно потому что ⁡ ( ϕ м ) N π 180 {\ displaystyle K_ {2} = \ cos (\ phi _ {m}) N {\ frac {\ pi} {180}} \, \!} = километров на градус разницы долготы;

где и являются м eridional и его перпендикулярен, или « п НПУ », (выражения в формуле FCC являются производными от биномиальной серии формы расширения и , набора к Кларку 1866 г. эллипсоиду ). M {\ Displaystyle M \, \!} N {\ Displaystyle N \, \!} M {\ Displaystyle M \, \!} N {\ Displaystyle N \, \!}

Для более эффективной с вычислительной точки зрения реализации вышеприведенной формулы несколько приложений косинуса можно заменить одним приложением и использованием рекуррентного соотношения для полиномов Чебышева .

Формула плоской Земли в полярных координатах

D знак равно р θ 1 2 + θ 2 2 — 2 θ 1 θ 2 потому что ⁡ ( Δ λ ) , {\ displaystyle D = R {\ sqrt {\ theta _ {1} ^ {2} \; {\ boldsymbol {+}} \; \ theta _ {2} ^ {2} \; \ mathbf {-} \; 2 \ theta _ {1} \ theta _ {2} \ cos (\ Delta \ lambda)}},}

где значения ширины в радианах. Для широты, измеряемой в градусах, широта в радианах может быть вычислена следующим образом: θ знак равно π 180 ( 90 ∘ — ϕ ) . {\ displaystyle \ theta = {\ frac {\ pi} {180}} (90 ^ {\ circ} — \ phi). \, \!}

Двусторонний спутниковый Интернет

Что такое географические координаты?

Географические координаты определяют положение точки на земной поверхности. Географические координаты строятся по принципу сферических и состоят из широты и долготы.

Широта — угол между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° в обе стороны от экватора. Географическую широту точек, лежащих в северном полушарии, (северную широту) принято считать положительной, широту точек в южном полушарии — отрицательной. О широтах, близких к полюсам, принято говорить как о высоких, а о близких к экватору — как о низких.

Долгота — угол между плоскостью меридиана, проходящего через данную точку, и плоскостью начального нулевого меридиана, от которого ведётся отсчёт долготы. Долготы от 0° до 180° к востоку от нулевого меридиана называют восточными, к западу — западными. Восточные долготы принято считать положительными, западные — отрицательными.

Формат записи географических координат

Географические координаты одной точки могут быть выражены в разных форматах. В зависимости от того, представлены минуты и секунды как значения от 0 до 60 или от 0 до 100 (десятичные доли).

Формат координат обычно записывают следующим образом: DD — градусы, MM — минуты, SS — секунды, если минуты и секунды представлены как десятичные доли, то пишут просто DD.DDDD. Например:

1. DD MM SS: 50° 40′ 45» в.д., 40 50′ 30» с.ш. — градусы, минуты, секунды
2. DD MM.MM: 50° 40.75′ в.д., 40 50.5′ с.ш. — градусы, десятичные минуты
3. DD.DDDDD: 50.67916 в.д., 40.841666 с.ш. — десятичные градусы

Для чего нужно знать координаты своего дома

Зачастую дома в дачных поселках и многих деревнях не имеют четкой навигации состоящей из вывесок с названиями улиц и нумерации домов или даже дома имея вывески с номерами могут быть раскиданы по всему поселку в случайном порядке (исторически сложившемуся по мере застройки поселка). Бывают случаи, что с навигацией в населенном пункте все хорошо, но не во всех автомобильных GPS-навигаторах такой дом или улица находится. Жителям таких домов приходится долго и, как правило, запутанно объяснять как до них добраться используя разные ориентиры. В таком случае проще дать координаты дома, ведь любой автомобильный навигатор может проложить путь по координатам.

Для проработки технической возможности подключения Интернета в загородном доме мы также просим своих заказчиков предоставить координаты дома, особенно в том случае если ни на одном из картографических онлайн-сервисов он не находится по адресу.

Определение координат с помощью картографических онлайн-сервисов

В настоящее время самыми известными картографическими онлайн-сервисами с функцией поиска являются карты Google и Yandex. Рассмотрим, как можно определить географические координаты по карте или снимку со спутника в сервисе Maps:

1. Откройте Карты Google https://maps.google.ru

2. Найдите на карте точное место. Для этого карту можно двигать мышью, приближать и удалять прокручивая колесико мыши. Также можно найти нужный населенный пункт с помощью поиска по названию используя населенный пункт, улицу и дом. Чтобы максимально точно найти место дома переключайтесь между режимами отображения: Карта, Гибрид или Спутник.

3. Щелкните правой кнопкой мыши по нужному месту на карте и выберите из открывшегося меню пункт “Что тут находится?”. На карте появится маркер в виде зеленой стрелки. Повторите операцию, если маркер установился неточно.

4. При наведении мыши на зеленую стрелку появятся географические координаты места, также они появятся и в строке поиска откуда их можно скопировать в буфер обмена.

Рис. 1. Определение координат места по указателю на карте Google

Теперь рассмотрим как можно определить географические координаты по карте или снимку со спутника в сервисе Яндекс.Карты:

Для поиска места применим тот же алгоритм, что и для поиска на картах Google. Откройте Яндекс.Карты: https://maps.yandex.ru. Для получения координат на Яндекс-карте используется инструмент «Получить информацию» (кнопка со стрелкой и знаком вопроса, в левой верхней части карты). При щелчке этим инструментом по карте на ней появляется маркер, а в строке поиска отображаются координаты.

Рис. 2. Определение координат места по указателю на Яндекс-карте

На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаками «-» для отрицательной долготы. На картах Google и картах Яндекс вначале широта, затем долгота (до октября 2012 на картах Яндекс был принят обратный порядок: сначала долгота, потом широта).

Работа с картами 1С 4 в 1: Яндекс, Google , 2ГИС, OpenStreetMap(OpenLayers) Промо

С каждым годом становится все очевидно, что использование онлайн-сервисов намного упрощает жизнь. К сожалению по картографическим сервисам условия пока жестковаты. Но, ориентируясь на будущее, я решил показать возможности API выше указанных сервисов:
Инициализация карты
Поиск адреса на карте с текстовым представлением
Геокодинг
Обратная поиск адреса по ее координатами
Взаимодействие с картами — прием координат установленного на карте метки
Построение маршрутов по указанным точками
Кластеризация меток на карте при увеличении масштаба
Теперь также поддержка тонкого и веб-клиента

1 стартмани

Система координат

Прежде чем говорить о расстоянии между точками по координатам, следует ввести систему отчета, в которой каждый геометрический объект можно будет однозначно определять. Для этой цели часто используют декартову систему координат. Она представляет собой взаимно перпендикулярные прямые, на каждой из которых отмечены единичные отрезки. Именно в них определяется положение тел в пространстве, на плоскости или на прямой линии.

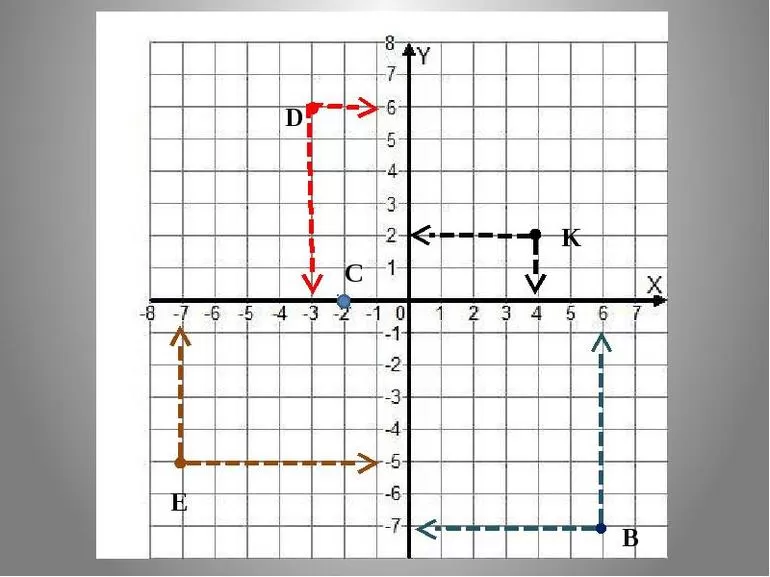
Для названных трех случаев декартова система координат отличается количеством осей:

• 3 для определения положения пространственных объектов;
• 2 для фигур на плоскости;
• 1 для вычисления координат точек.

Единичные отрезки на координатных осях в общем случае могут иметь разную длину.

Как пользоваться расчетом расстояний?

Для того чтобы рассчитать маршрут между городами,
начните вводить в поле «Откуда» название начального пункта маршрута.
Из выпадающей контекстной подсказки выберите нужный город.
По аналогии заполните поле «Куда» и нажмите кнопку «рассчитать».

На открывшейся странице на карте будет проложен маршрут, красными маркерами будут обозначены начальный и конечный
населенные пункты, а красной линией будет показан путь по автодороге.
Над картой будут указаны суммарная длина маршрута, продолжительность пути и расход топлива.
Под этой информацией будет размещена сводная таблица с подробными данными о маршруте и об участках пути: тип дороги,
расчетная длина и продолжительность каждого фрагмента маршрута.

Полученный маршрут можно распечатать или, изменив некоторые параметры, повторить расчет.
В дополнительных настройках можно задать транзитные населенные пункты, а также скорректировать расчетную скорость
движения по дорогам каждого типа.
Ниже дополнительных настроек расположены поля ввода данных топливного калькулятора.
Внесите в них актуальный расход горючего вашей машины и среднюю цену 1 литра топлива.
При повторном расчете эти данные будут использованы для подсчета необходимого количества топлива и его стоимости.

Как рассчитать азимут (угол к северу) между двумя координатами WGS84

У меня есть две координаты WGS84, широта и долгота в градусах. Эти точки расположены довольно близко друг к другу, например, всего в одном метре друг от друга.

• есть ли простой способ рассчитать Азимут линии между этими точками, то есть угол к северу?
• наивным подходом было бы предположить декартову систему координат (потому что эти точки так близко друг к другу) и просто использовать
• sin (a) = abs (L2 — L1) / sqrt(sqr(L2-L1) + sqr (B2-B1))
• a = Азимут
  Л1, Л2 = долготы
  Б1, Б2 = широте
• ошибка будет больше, поскольку координаты удаляются от экватора, потому что там расстояние между двумя продольными градусами становится все меньше, чем расстояние между двумя широтными градусами (которое остается постоянным).
• Я нашел некоторые довольно сложные формулы, которые я действительно не хочу реализовывать, потому что они кажутся излишними для точек, которые так близко друг к другу, и я не нужна очень высокая точность (достаточно двух десятичных знаков, один, вероятно, прекрасен, так как есть другие факторы, которые уменьшают точность в любом случае, например, тот, который возвращает GPS).
• возможно, я мог бы просто определить приблизительный коэффициент продольной коррекции в зависимости от широты и использовать что-то вроде этого:
• sin (a) = abs(L2*f-L1*f) / sqrt(sqr(L2*f-L1*f) + sqr(B2-B1))
• где F-поправочный коэффициент
• какие-то намеки?

(Я не для этого необходимо использовать любые библиотеки, особенно те, которые требуют лицензий среды выполнения. Любой источник Mpled Delphi будет отличным.)

delphi geolocation geospatial

формулы, на которые вы ссылаетесь в тексте, предназначены для вычисления большого расстояния окружности между 2 точками. Вот как я вычисляю угол между точками:

uses Math, …;
…

const
cNO_ANGLE=-999;

…

function getAngleBetweenPoints(X1,Y1,X2,Y2:double):double;
var
dx,dy:double;
begin
dx := X2 — X1;
dy := Y2 — Y1;

if (dx > 0) then result := (Pi*0.5) — ArcTan(dy/dx) else
if (dx 0) then result := 0 else
if (dy

Не забудьте обработать ситуацию, когда 2 точки равны (проверьте, равен ли результат cNO_ANGLE, или измените функцию, чтобы вызвать исключение);
эта функция предполагает, что вы находитесь на плоской поверхности. С небольшими расстояниями, о которых вы упомянули, это все. хорошо, но если вы собираетесь вычислять заголовок между городами по всему миру, вы можете посмотреть на что-то, что принимает форму Земли в графе;
лучше всего предоставить этой функции координаты, которые уже сопоставлены с плоской поверхностью. Вы можете подать широту WGS84 непосредственно в Y (и lon в X), чтобы получить грубое приближение.

вот решение C#. Испытания для 0, 45, 90, 135, 180, 225, 270 и 315 углы.

редактировать Я заменил свое предыдущее уродливое решение переводом решения Ваутера на C#:

public double GetAzimuth(LatLng destination)
{
var longitudinalDifference = destination.Lng — this.Lng;
var latitudinalDifference = destination.Lat — this.Lat;
var azimuth = (Math.PI * .5d) — Math.Atan(latitudinalDifference / longitudinalDifference);
if (longitudinalDifference > 0) return azimuth;
else if (longitudinalDifference Это будет работать только для небольших различиях. В противном случае вы не можете просто «latitudinalDifference / longitudinalDifference».

Я бы рекомендовал реализовать поправочный коэффициент, основанный на долготе. Однажды я внедрил процедуру simular, чтобы вернуть все геокодированные записи в пределах x миль от определенного места и столкнулся с проблемами simular. К сожалению, у меня больше нет кода, и я не могу вспомнить, как я добрался до номера исправления, но вы на правильном пути.

Формулы

Существует три способа расчета сферического расстояния большого круга.

1. Сферическая теорема косинусов

В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением.

φ1, λ1; φ2, λ2 — широта и долгота двух точек в радианах

Δλ — разница координат по долготе

Δδ — угловая разница

Δδ = arccos {sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ}

Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).

Используется, чтобы избежать проблем с небольшими расстояниями.

3. Модификация для антиподов

Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.

Навигатор по конфигурации базы 1С 8.3 Промо

Универсальная внешняя обработка для просмотра метаданных конфигураций баз 1С 8.3.
Отображает свойства и реквизиты объектов конфигурации, их количество, основные права доступа и т.д.
Отображаемые характеристики объектов: свойства, реквизиты, стандартные рекизиты, реквизиты табличных частей, предопределенные данные, регистраторы для регистров, движения для документов, команды, чужие команды, подписки на события, подсистемы.
Отображает структуру хранения объектов базы данных, для регистров доступен сервис «Управление итогами».
Платформа 8.3, управляемые формы. Версия 1.1.0.83 от 24.06.2021

3 стартмани

Расстояние между Q и прямой

Полученные знания можно с легкостью применять для решения разнообразных задач по геометрии. Часто приходится находить дистанцию между точкой и прямой. Определить эту величину можно, если знать направляющий вектор прямой. Предположим, что он имеет следующие координаты: a- (x1; y1). Прямая проходит через A (x2; y2). Точка задается так: Q (x0; y0).

В параметрическом виде прямая записывается следующим образом:

Здесь t — параметр, который может принимать любое действительное число. Это выражение позволяет записать равенство (1):

Пусть точка P (x;y) является проекцией Q (x0;y0) на прямую, тогда расстояние PQ является искомой дистанцией, которую следует найти по условию задачи. Поскольку вектора PQ- и a- перпендикулярны друг другу, их скалярное произведение будет равно нулю (угол между векторами равен 90 градусов, его косинус равен нулю). Исходя из этих рассуждений, можно записать выражение (2):

Поскольку имеющиеся равенства (1) и (2) содержат 2 неизвестные переменные, объединение их в систему и решение ее позволит определить точку P (x;y). Зная ее координаты и используя формулу дистанции между двумя точками на плоскости, можно получить искомое расстояние PQ.

Расстояние от точки до прямой в пространстве – теория, примеры, решения.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz, задана точка , прямая a и требуется найти расстояние от точки А до прямой a.

Покажем два способа, позволяющих вычислять расстояние от точки до прямой в пространстве. В первом случае нахождение расстояния от точки М₁ до прямой a сводится к нахождению расстояния от точки М₁ до точки H₁, где H₁ — основание перпендикуляра, опущенного из точки М₁ на прямую a. Во втором случае расстояние от точки до плоскости будем находить как высоту параллелограмма.

Итак, приступим.

Первый способ нахождения расстояния от точки до прямой a в пространстве.

Так как по определению расстояние от точки М₁ до прямой a – это длина перпендикуляра M₁H₁, то, определив координаты точки H₁, мы сможем вычислить искомое расстояние как расстояние между точками и по формуле .

Таким образом, задача сводится к нахождению координат основания перпендикуляра, построенного из точки М₁ к прямой a. Сделать это достаточно просто: точка H₁ – это точка пересечения прямой a с плоскостью, проходящей через точку М₁ перпендикулярно к прямой a.

Следовательно, алгоритм, позволяющий определять расстояние от точки до прямой a в пространстве, таков:

• составляем уравнение плоскости как уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой a;
• определяем координаты точки H₁ – точки пересечения прямой a и плоскости (смотрите статью нахождение координат точки пересечения прямой и плоскоти);
• вычисляем требуемое расстояние от точки М₁ до прямой a по формуле .

Второй способ, позволяющий находить расстояние от точки до прямой a в пространстве.

Так как в условии задачи нам задана прямая a, то мы можем определить ее направляющий вектор и координаты некоторой точки М₃, лежащей на прямой a. Тогда по координатам точек и мы можем вычислить координаты вектора : (при необходимости обращайтесь к статье координаты вектора через координаты точек его начала и конца).

Отложим векторы и от точки М₃ и построим на них параллелограмм. В этом параллелограмме проведем высоту М₁H₁.

Очевидно, высота М₁H₁ построенного параллелограмма равна искомому расстоянию от точки М₁ до прямой a. Найдем .

С одной стороны площадь параллелограмма (обозначим ее S) может быть найдена через векторное произведение векторов и по формуле . С другой стороны площадь параллелограмма равна произведению длины его стороны на высоту, то есть, , где — длина вектора , равная длине стороны рассматриваемого параллелограмма. Следовательно, расстояние от заданной точки М₁ до заданной прямой a может быть найдена из равенства как .

Итак, чтобы найти расстояние от точки до прямой a в пространстве нужно

• определить направляющий вектор прямой a () и вычислить его длину ;
• получить координаты некоторой точки М₃, лежащей на прямой a, вычислить координаты вектора , найти векторное произведение векторов и как и получить его длину ;
• вычислить требуемое расстояние от точки до прямой в пространстве по формуле .

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве.

Рассмотрим решение примера.

Пример.

Найдите расстояние от точки до прямой .

Решение.

Первый способ.

Напишем уравнение плоскости , проходящей через точку М₁ перпендикулярно заданной прямой:

Найдем координаты точки H₁ — точки пересечения плоскости и заданной прямой. Для этого выполним

после чего решим систему линейных уравнений методом Крамера:

Таким образом, .

Осталось вычислить требуемое расстояние от точки до прямой как расстояние между точками и :.

Второй способ.

Числа, стоящие в знаменателях дробей в канонических уравнениях прямой, представляют собой соответствующие координаты направляющего вектора этой прямой, то есть, — направляющий вектор прямой . Вычислим его длину: .

Очевидно, что прямая проходит через точку , тогда вектор с началом в точке и концом в точке есть . Найдем векторное произведение векторов и :
тогда длина этого векторного произведения равна .

Теперь мы располагаем всеми данными, чтобы воспользоваться формулой для вычисления расстояния от заданной точки до заданной плоскости: .

Ответ:

.

Список литературы.

• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
• Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Ильин В.А., Позняк Э.Г. Аналитическая геометрия.

Некогда разбираться?

Пример задачи

Применить полученные знания поможет простая геометрическая проблема. Имеется прямая, которая задана на плоскости в виде следующего общего выражения:

Пусть проекцией точки Q на прямую будет нульмерный объект P (x;y). Координаты P должны удовлетворять записанному уравнению.

Чтобы определить направляющий вектор, достаточно взять 2 любые точки на прямой. Подставляя в выражение произвольные значения x, можно определить эти точки A, B и вместе с ними направляющий вектор AB-:

Вектор QP-, который пересекает прямую под прямым углом, должен подчиняться следующему уравнению (свойство скалярного произведения):

В это выражение нужно подставить значение y из уравнения прямой.

Получается:

Таким образом, значение координат проекции Q на прямую равны: P (1,1; -2,3). Остается применить формулу для дистанции между P и Q, чтобы получить ответ на поставленную задачу:

Рассчитанное значение округлено до сотых долей и выражается в единицах единичных векторов координатной системы.

При решении подобных задач для сокращения последующих вычислений рекомендуется проверять принадлежность точки прямой, для чего следует подставить координаты в уравнение. Если этот факт подтверждается, искомое расстояние равно нулю.

Обработка «Распознавание штрихкода с помощью утилиты Zbar» для Документооборот ред. 2 Промо

В связи с тем, что стандартный функционал программы «Документооборот» ред. 2.1 дает возможность распознавания штрихкодов только форма EAN-13, данная обработка — альтернативный способ для распознавания штрихкода в программе 1С: Документооборот ред. 2 с помощью утилиты Zbar, которая распознает в том числе и в формате Code 128 (один из стандартных штрихкодов кодирования документов, например, «Управление торговлей» ред. 11), а также с возможностью поэтапно проследить все действия от распознавания до прикрепления к документу или простой загрузки в каталоги файлов в базе 1С.

5 стартмани

АЗИМУТ

Азимут, магнитный и истинный — угол, образуемый в данной точке на местности или на карте направлением на север и на какой- либо предмет.

Азимутом пользуются для ориентирования при передвижении в лесу, в горах, в песчаной пустыне или в условиях плохой видимости (ночью, при сильном тумане), когда сличить карту с местностью и ориентироваться по ней трудно, а порой и невозможно.

С помощью азимута определяют также направление движения судов в море и самолетов.

На местности отсчет азимутов производится от направления стрелки компаса (ее северного конца) по ходу часовой стрелки от 0° до 360°, иначе говоря — от магнитного меридиана данной точки. Если предмет находится от наблюдателя точно к северу, то азимут его 0°, если на востоке—90°, на юге—180°, на западе — 270°. При наблюдении по компасу измеряется магнитный азимут.

Для определения магнитного азимута компас располагают так, чтобы нулевое деление на циферблате и буква «С» указывали точно на север, т. е. ориентируют компас по сторонам горизонта. Желательно при этом, чтобы компас помещался на высоком пне или на торце вертикально вбитого в землю кола.

Следя за тем, чтобы коробка компаса оставалась неподвижной и стрелка не отходила от нулевого деления, вращают визирное приспособление и наводят мушку на предмет, азимут которого надо определить. Замечают, около какой цифры на лимбе (разделенном на градусы круге) остановился при этом указатель. Отсчет по указателю (в градусах) равен азимуту данного предмета. Если компас не имеет визирного приспособления, его можно заменить тонкой палочкой, которую кладут на стекло компаса так, чтобы она проходила через центр циферблата и была направлена на предмет, азимут которого надо определить.

На рисунке показаны примеры определения азимутов на некоторые местные предметы: на вышку азимут равен 0°, на отдельно стоящее дерево — 50°, на дом — 295°.

Движение по азимуту

. Иногда бывает необходимо дойти до какого-то предмета на местности и возвратиться обратно. Чтобы знать, по какому азимуту следует идти обратно, надо к найденному азимуту прибавить 180°. Получим обратный азимут. Например, если от моста до дерева следует двигаться по азимуту 50°, то обратно—по азимуту 230° (50° +180°=230°). Если при расчете обратного азимута сумма углов окажется больше 360°, то эта величина (360°) отбрасывается. Например, прямой азимут от моста до дома равен 295°, а обратный — 115° (295° +180°-360° = 115°).

Случается, что предмет, до которого необходимо дойти по данному азимуту, не виден наблюдателю (за лесом, холмом). Поступают так. Находят по компасу нужный азимут и стараются отыскать в этом направлении какой-нибудь ориентир (высокое дерево, курган, вышку). Убирают компас и двигаются в направлении ориентира. Дойдя до него, снова определяют этот же азимут и продолжают движение. Бывает, что на пути встретилось болото или озеро. Тогда по компасу определяют нужный азимут и стараются отыскать ориентир на противоположной стороне. Затем компас убирают и движутся в обход встретившегося препятствия. Дойдя до выбранного ориентира, по компасу определяют азимут и продолжают движение.

Двигаясь по лесу, компас держат на ладони перед собой так, чтобы нулевое деление все время совпадало с северным концом стрелки.

Определение азимута по карте

. Азимут определяют и по карте. Предположим, во время похода краеведам надо пройти от лагеря до сторожки лесника, которая находится в 5 км от него. Для определения азимута по карте пользуются транспортиром. В нашем примере азимут от лагеря до сторожки лесника равен 55°. После того как азимут по карте определен, на местности находят его по компасу и идут в нужном направлении.

Азимутальная съемка

. С помощью компаса можно составить план небольшого участка местности. Для этого из какой-то определенной точки (в нашем примере от моста) определяют азимуты до видимых местных предметов, измеряют до них расстояния и данные заносят в таблицу:

Затем на листе бумаги ставят точку, от которой определяли азимуты и расстояния до местных предметов; от нее с помощью транспортира откладывают азимуты и в определенном масштабе расстояния до предметов, которые обозначаются принятыми условными знаками.

Формула расчета расстояния по координатам

Пусть и являются географическими широтой и долготой двух точек 1 и 2, и — их абсолютная разность. Тогда , центральный угол между ними, определяется теоремой сферических косинусов:

Формула расстояние d т.е.длины дуги, для сферы радиуса R и приведены в радианах

Больше матиматики .

На компьютерных системах с низкой точностью с плавающей запятой, эта формула может иметь большие ошибки округления, если расстояние не большое (если две точки находятся в 1 км друг от друга на поверхности Земли, косинус центрального угла выходит 0,99999999). Для современных 64-разрядных чисел с плавающей запятой, формула Теоремы косинусов, которая приведенна выше, не имеет серьезных ошибок округления для расстояний более нескольких метров на поверхности Земли. Эта формула лучше подходит для вычисления растояние по координатам на небольшые расстояния

Для получения более точных рузультатов на большых расстояниях стараются исполтзовать формулу посложнее, в которой сделано предположение, что сфера является эллипсоидом с одинаковыми большой и малой осями.

Источник

Расстояние между двумя точками на поверхности Земли

Представим, что для чего-то понадобилось измерить расстояние между двумя точками на поверхности Земли, например, расстояние между Красной площадью и Эрмитажем. Конечно, можно попробовать решить задачу в лоб и посчитать евклидово расстояние по формуле:

но этот подход не заработает по той простой причине, что евклидова метрика предназначена для вычисления расстояния на плоскости, а поверхность Земли — это всё-таки фигура, очень близкая к сфере.

Для решения такой задачи нужно обратиться к редко используемым тригонометрическим функциям.

Одна из таких функций, называется синус-верзус, или, по-другому, версинус. Он представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Вычисляется версинус по формуле:

Гаверсинус — это просто половина версинуса, и именно эта функция поможет нам в решении задачи с поиском расстояния:

Для любых двух точек на сфере гаверсинус центрального угла между ними вычисляется по формуле:

• d — это центральный угол между двумя точками, лежащими на большом круге
• r — радиус сферы
• φ₁ и φ₂ — широта первой и второй точек в радианах
• λ₁ и λ₂ — долгота первой и второй точек в радианах

Обозначим временно гаверсинус отношения длины к радиусу как переменную h:

Тогда длину d можно вынести за знак равенства:

а для того, чтобы избавиться от дроби, выразим гаверсинус через арксинус:

затем раскроем переменную h:

подставим формулу гаверсинуса и получим формулу вычисления расстояния:

Теперь вернёмся к исходной задаче поиска расстояния между Красной площадью и Эрмитажем.

Для Красной площади Гугл подсказал координаты (55.7539° N, 37.6208° E), а для Эрмитажа — (59.9398° N, 30.3146° E).

Прежде, чем подставлять координаты в формулу, их нужно перевести в радианы.

Для того, чтобы вычислить длину, нужно полученное значение арксинуса умножить на два радиуса сферы. Подсчёты усложняет тот факт, что Земля не является идеальной сферой и её радиус немного варьируется. Воспользуемся усреднённым значением радиуса, которое, в соответствии со стандартом WGS84 приблизительно равно 6371 км:

Произведя умножение, получаем искомое значение, которое приблизительно равно 634.57 км.

Кстати, из-за того, что Земля — не идеальная сфера, погрешность расчётов с использованием этой формулы, составляет около 0,5%.

Источник

Когда может пригодиться расчет расстояний?

Бесплатный расчет расстояний между городами показывает точное расстояние между городами и считает кратчайший маршрут с расходом топлива.
Он может быть востребован в следующих случаях:

• Сервис расчета расстояний помогает проложить маршрут автопутешественнику, например, для летнего отдыха с семьей
  или при планировании деловой поездки на автомобиле.
  Зная расход бензина и среднюю цену за литр топлива, нетрудно рассчитать обязательные финансовые затраты в поездке.
• Водителю-дальнобойщику расчет расстояния между городами позволяет проложить маршрут на карте при
  подготовке к дальнему рейсу.
• Калькулятор расстояний пригодится грузоотправителю, чтобы определить километраж и в соответствии
  с тарифами транспортной компании оценить стоимость грузоперевозки.