Расстояние от точки до плоскости

Другие методы прокладки маршрута

Пожалуй, самая простая альтернатива — это открыть атлас автодорог и на глаз проложить маршрут по карте.
Затем, прокатив по маршруту курвиметр, можно получить приблизительный километраж.
Оценить время поездки будет сложнее: для этого придется разбить маршрут на фрагменты с одинаковым классом дорог и
измерить сумму длин фрагментов каждого класса.
Далее, зная среднюю скорость для каждого класса дорог, нетрудно рассчитать время, поделив путь на скорость.

Если курвиметра нет под рукой, то можно воспользоваться линейкой.
Приложите нулевую отметку линейки к начальному пункту маршрута и двигайте линейку, плотно примыкая ее к извилинам
дороги.

Рассчитать расстояние между городами также можно с помощью таблиц, которые опубликованы в атласах и
справочниках.
Это достаточно удобно для маршрутов, начинающихся и заканчивающихся в крупных городах.
Мелких населенных пунктов, как правило, нет в таблицах.

Расстояние между двумя точками на поверхности Земли

Представим, что для чего-то понадобилось измерить расстояние между двумя точками на поверхности Земли, например, расстояние между Красной площадью и Эрмитажем. Конечно, можно попробовать решить задачу в лоб и посчитать евклидово расстояние по формуле:

но этот подход не заработает по той простой причине, что евклидова метрика предназначена для вычисления расстояния на плоскости, а поверхность Земли — это всё-таки фигура, очень близкая к сфере.

Для решения такой задачи нужно обратиться к редко используемым тригонометрическим функциям.

Одна из таких функций, называется синус-верзус, или, по-другому, версинус. Он представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Вычисляется версинус по формуле:

Гаверсинус — это просто половина версинуса, и именно эта функция поможет нам в решении задачи с поиском расстояния:

Для любых двух точек на сфере гаверсинус центрального угла между ними вычисляется по формуле:

• d — это центральный угол между двумя точками, лежащими на большом круге
• r — радиус сферы
• φ₁ и φ₂ — широта первой и второй точек в радианах
• λ₁ и λ₂ — долгота первой и второй точек в радианах

Обозначим временно гаверсинус отношения длины к радиусу как переменную h:

Тогда длину d можно вынести за знак равенства:

а для того, чтобы избавиться от дроби, выразим гаверсинус через арксинус:

затем раскроем переменную h:

подставим формулу гаверсинуса и получим формулу вычисления расстояния:

Теперь вернёмся к исходной задаче поиска расстояния между Красной площадью и Эрмитажем.

Для Красной площади Гугл подсказал координаты (55.7539° N, 37.6208° E), а для Эрмитажа — (59.9398° N, 30.3146° E).

Прежде, чем подставлять координаты в формулу, их нужно перевести в радианы.

Для того, чтобы вычислить длину, нужно полученное значение арксинуса умножить на два радиуса сферы. Подсчёты усложняет тот факт, что Земля не является идеальной сферой и её радиус немного варьируется. Воспользуемся усреднённым значением радиуса, которое, в соответствии со стандартом WGS84 приблизительно равно 6371 км:

Произведя умножение, получаем искомое значение, которое приблизительно равно 634.57 км.

Кстати, из-за того, что Земля — не идеальная сфера, погрешность расчётов с использованием этой формулы, составляет около 0,5%.

Источник

Декартовы координаты

Линия, определяемая уравнением

В случае прямой на плоскости, заданной уравнением ax + by + c = 0 , где a , b и c — действительные константы, причем a и b не равны нулю, расстояние от прямой до точки ( x , y ) является

расстояние⁡(аИкс+бу+cзнак равно,(Икс,у))знак равно|аИкс+бу+c|а2+б2.{\ displaystyle \ operatorname {distance} (ax + by + c = 0, (x_ {0}, y_ {0})) = {\ frac {| ax_ {0} + by_ {0} + c |} {\ sqrt {a ^ {2} + b ^ {2}}}}.}

Точка на этой прямой, ближайшая к ( x , y ), имеет координаты:

Иксзнак равноб(бИкс-ау)-аcа2+б2 а также узнак равноа(-бИкс+ау)-бcа2+б2.{\ displaystyle x = {\ frac {b (bx_ {0} -ay_ {0}) — ac} {a ^ {2} + b ^ {2}}} {\ text {and}} y = {\ frac) {a (-bx_ {0} + ay_ {0}) — bc} {a ^ {2} + b ^ {2}}}.}

Горизонтальные и вертикальные линии

В общем уравнении линии ax + by + c = 0 , a и b не могут оба быть равными нулю, если c также не равно нулю, и в этом случае уравнение не определяет линию. Если a = 0 и b ≠ 0 , линия горизонтальна и имеет уравнение y = —cб. Расстояние от ( x , y ) до этой линии измеряется по отрезку вертикальной линии длиной | у — (-cб) | знак равно| от + с || б |в соответствии с формулой. Аналогично, для вертикальных линий ( b = 0) расстояние между той же точкой и линией равно| топор + с || а |, измеренный по горизонтальному отрезку.

Линия определяется двумя точками

Если прямая проходит через две точки P ₁ = ( x ₁ , y ₁ ) и P ₂ = ( x ₂ , y ₂ ), то расстояние ( x , y ) от прямой составляет:

расстояние⁡(п1,п2,(Икс,у))знак равно|(Икс2-Икс1)(у1-у)-(Икс1-Икс)(у2-у1)|(Икс2-Икс1)2+(у2-у1)2.{\ displaystyle \ operatorname {distance} (P_ {1}, P_ {2}, (x_ {0}, y_ {0})) = {\ frac {| (x_ {2} -x_ {1}) (y_ {1} -y_ {0}) — (x_ {1} -x_ {0}) (y_ {2} -y_ {1}) |} {\ sqrt {(x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2}}}}.}

Знаменателем этого выражения является расстояние между P ₁ и P ₂ . Числитель равен удвоенной площади треугольника с вершинами в трех точках ( x , y ) , P ₁ и P ₂ . См .: . Выражение эквивалентно h =2 Аб, которую можно получить, переписав стандартную формулу для площади треугольника: A =12 bh , где b — длина стороны, а h — высота перпендикуляра от противоположной вершины.

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

К ЕГЭ можно подготовиться . У нас на сайте полно качественных материалов. Но вы должны знать что вы делаете. 

• У вас должен быть план, чтобы вы шли от простого к сложному и не «захлебнулись». 
• Вас должен кто-то проверять и указывать короткий путь, чтобы вы не теряли время.
• Вас должен кто-то мотивировать, чтобы вы не бросили все.

Если у вас с этим сложности, приходите к нам.

• Начните с нашего гида о том как подготовиться к ЕГЭ по математике.
• Посетите наши бесплатные вебинары по математике, информатике и физике.

И если вам нужен действительно высокий балл, приходите на наши курсы: 

• Подготовка к ЕГЭ по математике
• Подготовка к ЕГЭ по информатике
• Подготовка к ЕГЭ по физике

Расстояние между координатами GPS

Для решения практических и теоретических задач в некоторых отраслях производства необходимо уметь определять расстояния между точками по их координатам. Для этого можно использовать несколько способов. Каноническая форма представления географических координат: градусы, минуты, секунды.

Для примера можно определить расстояние между следующими координатами: точка №1 — широта 55°45′07″ с.ш., долгота 37°36′56″ в.д.; точка №2 — широта 58°00′02″ с.ш., долгота 102°39′42″ в.д.

Наиболее простой способ — воспользоваться онлайн-калькулятором для расчета протяженности между двумя точками. В поисковике браузера необходимо задать следующие параметры для поиска: онлайн-калькулятор для расчета расстояния между двумя координатами. В онлайн-калькуляторе вводятся значения широт и долгот в поля запросов для первой и второй координаты. При расчете онлайн-калькулятор выдал результат – 3 800 619 м.

Следующий способ более трудоемкий, но и более наглядный. Необходимо воспользоваться любой доступной картографической или навигационной программой. К программам, в которых можно создать точки по координатам и измерить расстояния между ними, относятся следующие приложения: BaseCamp (современный аналог программы MapSource), «Google Планета Земля», «SAS.Планета».

Все вышеперечисленные программы доступны для любого пользователя сети. К примеру, для расчета расстояния между двумя координатами в программе «Google Планета Земля» необходимо создать две метки с указанием координат первой точки и второй точки. Затем при помощи инструмента «Линейка» нужно соединить линией первую и вторую метки, программа автоматически выдаст результат промера и покажет путь на спутниковом снимке Земли.

В случае с примером, приведенным выше, программа «Google Планета Земля» выдала результат – протяженность расстояния между точкой №1 и точкой №2 составляет 3 817 353 м.

Источник

Определение расстояния «на глаз» или по линейным объектам

Метод измерения расстояния «на глаз» подходит, когда есть объект с известным размером (длина, ширина или высота). Такой расчет считается точным на 90%, а иногда и больше, если набраться опыта.

Линейные размеры самых часто встречающихся объектов:

• легковой автомобиль — Д*Ш*В соответствует 4м*1,5м*1,6м;
• взрослый человек – в среднем 1,7 м;
• голова человека – В*Ш соответствует 0,25м*0,20м;
• столб связи (деревянный) – 6 м;
• столб связи (бетонный) – 8 м;
• расстояние между столбами ЛЭП – 50 м;
• между столбами высоковольтных линий – 100 м;
• деревенский дом – 7 м;
• один этаж многоквартирного дома (панельного) – 3 м.

LКак определять стороны света в природе, рассказываю в статье: Как определить север и юг без компаса днем и ночью

Как определить расстояние до объекта

Возьмите линейку и расположите ее на уровне измеряемого объекта в 50 см от глаз. Размеры предмета (длину, ширину или высоту) измеряют по линейке и учитывают в миллиметрах.

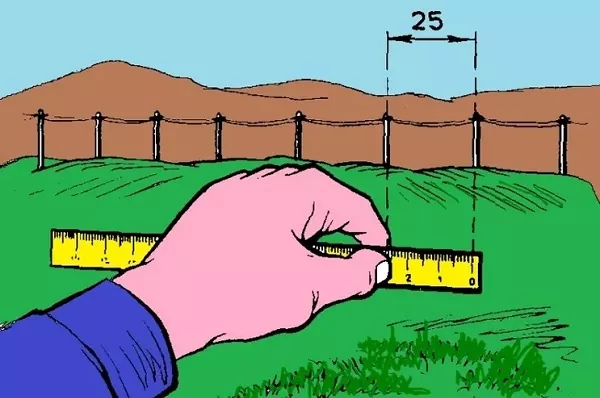
Определение расстояния по линейке

Теперь воспользуйтесь формулой:

Расстояние, м =(реальный размер в см/измеренный размер по линейке в мм)*5.

Этот академический метод в туристической среде был немного упрощен. Определение расстояния туристы проводят по большому пальцу.

Рассмотрим на примере измерения расстояния до столба связи (высота 8 м). Длина большого пальца около 6 см. Вытяните руку перед собой, сожмите ладонь в кулак так, чтобы большой палец смотрел вверх. Расстояние от глаз до пальца будет около 60 см. Определите какой длине соответствует столб, к примеру трети пальца (2 см).

Далее осталось рассчитать пропорцию:

Х = (8 м * 60 см)/2 см =240 м.

Расстояние между плоскостями − примеры и решения

Пример 1. Найти расстояние между плоскостями

и

Решение.

Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.

Общее уравнение плоскости имеет вид:

где n=(A,B,C)− называется нормальным вектором плоскости.

Нормальный вектор плоскости (7) равен n₁=(1, 2, −4), нормальный вектор плоскости (8′) равен n₂=(1, 2, −4). n₁=n₂. Следовательно эти плоскости параллельны.

Найдем расстояние между плоскостями (7) и (8′), используя следующую формулу:

Подставим значения A, B, C, D₁, D₂ в (9):

Упростим и решим:

Ответ. Расстояние между плоскостями равен:

Пример 2. Найти расстояние между плоскостями

и

Решение.

Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.

Пример 3. Найти расстояние между плоскостями

и

Решение.

Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.

Нормальный вектор плоскости (12) равен n₁=(4, 2, 8), нормальный вектор плоскости (13′) равен n₂=(4, 16/3, 64/3). n₁≠n₂. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.

Обзор и определения

Физические расстояния

Маршруты авиалиний между Лос-Анджелесом и Токио примерно следуют прямому маршруту большого круга (вверху), но при движении на восток следует использовать реактивный поток (внизу)

Обратите внимание, что кратчайший маршрут отображается в виде кривой, а не прямой линии, потому что эта карта является проекцией Меркатора , которая не масштабирует все расстояния одинаково по сравнению с реальной сферической поверхностью Земли.

« Манхэттенская дистанция » на сетке. Физическое расстояние может означать несколько разных вещей:

Физическое расстояние может означать несколько разных вещей:

• Пройденное расстояние: длина определенного пути, пройденного между двумя точками, например расстояние, пройденное при навигации по лабиринту.
• Прямолинейное (евклидово) расстояние: длина кратчайшего возможного пути в пространстве между двумя точками, который можно было бы пройти, если бы не было препятствий (обычно формализируется как евклидово расстояние ).
• Геодезическое расстояние: длина кратчайшего пути между двумя точками, оставаясь на некоторой поверхности, например, расстояние по дуге вдоль кривой Земли.
  
• Длина определенного пути, который возвращается к начальной точке, например, мяч, брошенный прямо вверх, или Земля, когда он завершает один оборот по орбите .

Доска с указанием расстояний до Вишакхапатнама

«Круговое расстояние» — это расстояние, пройденное колесом, которое может быть полезно при проектировании транспортных средств или механических передач. Окружность колеса равна 2 π  × радиус, и если принять радиус равным 1, то каждый оборот колеса эквивалентен расстоянию 2 π радиан. В технике часто используется ω  = 2 πƒ , где ƒ — частота .

Необычные определения расстояния могут быть полезны для моделирования определенных физических ситуаций, но также используются в теоретической математике:

• « Манхэттенское расстояние » — это прямолинейное расстояние, названное в честь количества кварталов (в северном, южном, восточном или западном направлениях), по которым такси должно проехать, чтобы добраться до пункта назначения на сетке улиц в некоторых частях Нью-Йорка. .
• «Расстояние до шахматной доски», формализованное как расстояние Чебышева , — это минимальное количество ходов, которое король должен сделать на шахматной доске , чтобы пройти между двумя клетками.

Меры расстояния в космологии усложняются расширением Вселенной и эффектами, описываемыми теорией относительности (такими как сокращение длины движущихся объектов).

Теоретические расстояния

Термин «расстояние» также используется по аналогии для измерения нефизических объектов определенными способами.

В информатике есть понятие « расстояние редактирования » между двумя строками. Например, слова «собака» и «точка», которые различаются только одной буквой, ближе, чем «собака» и «кошка», которые различаются на три буквы. Эта идея используется в средствах проверки орфографии и в теории кодирования и математически формализована несколькими различными способами, такими как:

• Расстояние Левенштейна
• Расстояние Хэмминга
• Расстояние Ли
• Расстояние Яро – Винклера

В математике метрическое пространство — это набор, для которого определены расстояния между всеми членами набора. Таким образом, можно вычислить множество различных типов «расстояний», например, для обхода графиков , сравнения распределений и кривых, а также с использованием необычных определений «пространства» (например, с использованием многообразия или отражений ). Понятие расстояния в теории графов использовалось для описания социальных сетей , например, с помощью числа Эрдёша или числа Бэкона — количество отношений сотрудничества на расстоянии от человека — от плодовитого математика Пола Эрдёша и актера Кевина Бэкона соответственно.

В психологии, географии человека и социальных науках расстояние часто рассматривается не как объективный показатель, а как субъективный опыт.

Расстояние между двумя параллельными плоскостями: определение

Определение 1

Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из рассматриваемых параллельных плоскостей до другой плоскости.

Пусть заданы две параллельные плоскости ϒ1 и ϒ2. Из произвольной точки М1плоскости ϒ1 опустим перпендикуляр М1Н1 на другую плоскость ϒ2. Длина перпендикуляра М1Н1 и будет являться расстоянием между заданными плоскостями.

Указанное определение расстояния между параллельными плоскостями имеет взаимосвязь со следующей теоремой.

Теорема

Если две плоскости параллельны, то все точки одной из параллельных плоскостей находятся на одном и том же расстоянии от другой плоскости.

Доказательство

Допустим, заданы две параллельные плоскости ϒ1 и ϒ2. Для получения доказательства теоремы необходимо доказать, что перпендикуляры, опущенные из различных произвольных точек одной плоскости к другой плоскости, равны. Пусть будут заданы некоторые произвольные точки М1 и М2 на плоскости ϒ1, и из них опущены перпендикуляры М1Н1 и М2Н2 на плоскость ϒ2. Таким образом, нам предстоит доказать, что М1Н1 = М2Н2.

Прямые М1Н1 и М2Н2 параллельны, поскольку перпендикулярны одной плоскости. Опираясь на аксиому о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, можем утверждать, что через две параллельные прямые проходит единственная плоскость. Будем считать, что существует некоторая плоскость ϒ3, проходящая через две параллельные прямые М1Н1 и  М2Н2. Очевидным фактом является то, что плоскость ϒ3 пересекает плоскости ϒ1 и ϒ2 по прямым М1M2 и Н1Н2, которые не пересекаются, а значит – параллельны (в ином случае, заданные плоскости имели бы общую точку, что невозможно в силу их параллельности по условию задачи). Таким образом, мы наблюдаем четырехугольник М1М2Н1Н2, у которого противоположные стороны являются попарно параллельными, т.е. М1М2Н1Н2 – параллелограмм (в рассматриваемом случае – прямоугольник). Следовательно, противоположные стороны у этого параллелограмма равны, а значит |М1Н1| = |М2Н2|. Что и требовалось доказать.

Заметим также, что расстояние между параллельными плоскостями – наименьшее из расстояний между произвольными точками этих плоскостей.

Расстояние от точки до прямой в пространстве – теория, примеры, решения.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz, задана точка , прямая a и требуется найти расстояние от точки А до прямой a.

Покажем два способа, позволяющих вычислять расстояние от точки до прямой в пространстве. В первом случае нахождение расстояния от точки М₁ до прямой a сводится к нахождению расстояния от точки М₁ до точки H₁, где H₁ — основание перпендикуляра, опущенного из точки М₁ на прямую a. Во втором случае расстояние от точки до плоскости будем находить как высоту параллелограмма.

Итак, приступим.

Первый способ нахождения расстояния от точки до прямой a в пространстве.

Так как по определению расстояние от точки М₁ до прямой a – это длина перпендикуляра M₁H₁, то, определив координаты точки H₁, мы сможем вычислить искомое расстояние как расстояние между точками и по формуле .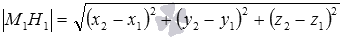

Таким образом, задача сводится к нахождению координат основания перпендикуляра, построенного из точки М₁ к прямой a. Сделать это достаточно просто: точка H₁ – это точка пересечения прямой a с плоскостью, проходящей через точку М₁ перпендикулярно к прямой a.

Следовательно, алгоритм, позволяющий определять расстояние от точки до прямой a в пространстве, таков:

• составляем уравнение плоскости как уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой a;
• определяем координаты точки H₁ – точки пересечения прямой a и плоскости (смотрите статью нахождение координат точки пересечения прямой и плоскоти);
• вычисляем требуемое расстояние от точки М₁ до прямой a по формуле .

Второй способ, позволяющий находить расстояние от точки до прямой a в пространстве.

Так как в условии задачи нам задана прямая a, то мы можем определить ее направляющий вектор и координаты некоторой точки М₃, лежащей на прямой a. Тогда по координатам точек и мы можем вычислить координаты вектора : (при необходимости обращайтесь к статье координаты вектора через координаты точек его начала и конца).

Отложим векторы и от точки М₃ и построим на них параллелограмм. В этом параллелограмме проведем высоту М₁H₁.

Очевидно, высота М₁H₁ построенного параллелограмма равна искомому расстоянию от точки М₁ до прямой a. Найдем .

С одной стороны площадь параллелограмма (обозначим ее S) может быть найдена через векторное произведение векторов и по формуле . С другой стороны площадь параллелограмма равна произведению длины его стороны на высоту, то есть, , где — длина вектора , равная длине стороны рассматриваемого параллелограмма. Следовательно, расстояние от заданной точки М₁ до заданной прямой a может быть найдена из равенства как .

Итак, чтобы найти расстояние от точки до прямой a в пространстве нужно

• определить направляющий вектор прямой a () и вычислить его длину ;
• получить координаты некоторой точки М₃, лежащей на прямой a, вычислить координаты вектора , найти векторное произведение векторов и как и получить его длину ;
• вычислить требуемое расстояние от точки до прямой в пространстве по формуле .

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве.

Рассмотрим решение примера.

Пример.

Найдите расстояние от точки до прямой .

Решение.

Первый способ.

Напишем уравнение плоскости , проходящей через точку М₁ перпендикулярно заданной прямой: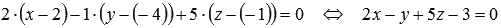

Найдем координаты точки H₁ — точки пересечения плоскости и заданной прямой. Для этого выполним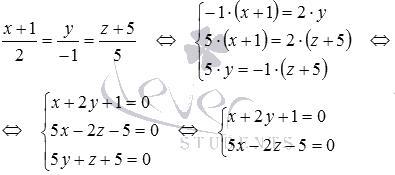

после чего решим систему линейных уравнений 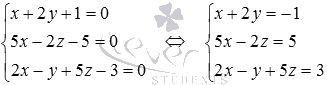методом Крамера: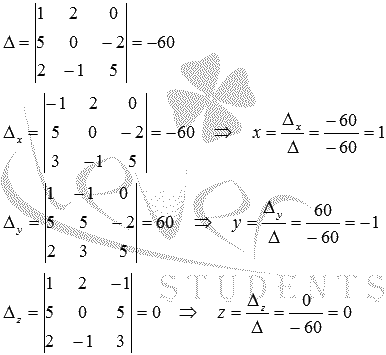

Таким образом, .

Осталось вычислить требуемое расстояние от точки до прямой как расстояние между точками и :.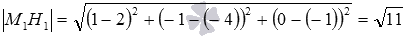

Второй способ.

Числа, стоящие в знаменателях дробей в канонических уравнениях прямой, представляют собой соответствующие координаты направляющего вектора этой прямой, то есть, — направляющий вектор прямой . Вычислим его длину: .

Очевидно, что прямая проходит через точку , тогда вектор с началом в точке и концом в точке есть . Найдем векторное произведение векторов и :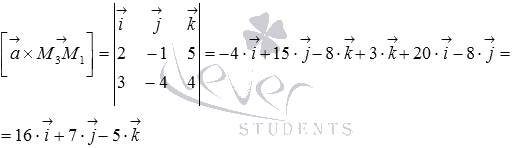
тогда длина этого векторного произведения равна .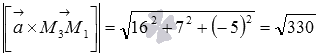

Теперь мы располагаем всеми данными, чтобы воспользоваться формулой для вычисления расстояния от заданной точки до заданной плоскости: .

Ответ:

.

Список литературы.

• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
• Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Ильин В.А., Позняк Э.Г. Аналитическая геометрия.

Некогда разбираться?

Переформулировка с использованием линейной алгебры

Формулу для ближайшей точки к началу координат можно выразить более кратко, используя обозначения линейной алгебры . Выражение в определении плоскости — это скалярное произведение , а выражение, появляющееся в решении, — это квадрат нормы . Таким образом, если является заданным вектором, плоскость может быть описана как набор векторов, для которых ближайшей точкой на этой плоскости является вектор
аИкс+бy+cz{\ displaystyle ax + by + cz} (а,б,c)⋅(Икс,y,z){\ Displaystyle (а, б, с) \ cdot (х, у, г)}а2+б2+c2{\ displaystyle a ^ {2} + b ^ {2} + c ^ {2}} |(а,б,c)|2{\ Displaystyle | (а, б, в) | ^ {2}}vзнак равно(а,б,c){\ Displaystyle \ mathbf {v} = (а, б, в)}ш{\ displaystyle \ mathbf {w}}v⋅шзнак равноd{\ Displaystyle \ mathbf {v} \ cdot \ mathbf {ш} = d}

пзнак равноvd|v|2{\ displaystyle \ mathbf {p} = {\ frac {\ mathbf {v} d} {| \ mathbf {v} | ^ {2}}}}.

Евклидово расстояние от начала координат до плоскости является нормой этой точки,

|d||v|знак равно|d|а2+б2+c2{\ displaystyle {\ frac {| d |} {| \ mathbf {v} |}} = {\ frac {| d |} {\ sqrt {a ^ {2} + b ^ {2} + c ^ {2 }}}}}.

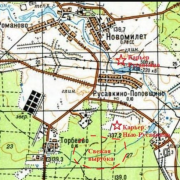
Измерить расстояние по карте

Для точного измерения расстояния на карте пользуются циркулем-измерителем, курвиметром и масштабной линейкой. Циркуль-измеритель должен без труда разводиться и сохранять приданное положение, а его острие – давать тонкий накол.

Курвиметр применяется для измерения длин кривых линий. Устроен он просто: колесико, находящееся внизу, соединено системой зубчатых передач со стрелкой, которая при движении колесика вдоль измеряемой на карте линии вращается и указывает отсчет на шкале циферблата.

У некоторых курвиметров вместо стрелки вращается циферблат. На этих устройствах шкала имеется с двух сторон: на одной стороне – в сантиметрах, а на другой – в дюймах.

Чтобы установить соответствие цены деления измеряемой величине, следует измерить известную длину какой-нибудь линии и сравнить.

Измерение расстояний на карте с помощью циркуля и линейного масштаба выполняется в следующем порядке. Допустим, нужно определить расстояние между двумя точками А и В.

Раствором циркуля зафиксируем это расстояние и, не меняя раствора, перенесем циркуль на линейный масштаб так, чтобы одна ножка точно совпала с нулем или с подписанным делением вправо от нуля, а другая встала влево от нуля. Произведя отсчет по делениям масштаба, определим, что измеренное расстояние между точками А и В равно 290 м.

Держать циркуль при измерениях следует всегда правой рукой с небольшим наклоном от себя, причем так, чтобы его ножки только слегка прикасались к делениям масштаба.

Для определения расстояния на карте с помощью курвиметра нужно предварительно совместить его стрелку с начальным делением шкалы циферблата, а затем установить колесико в исходной точке и осторожным движением прокатить курвиметр вдоль измеряемой кривой линии до конечной точки.

При движении курвиметра необходимо следить, чтобы стрелка вращалась в правильном направлении. Если курвиметр имеет шкалу, выраженную в километрах, измеренное расстояние следует отсчитывать по делениям, соответствующим масштабу карты.

Так как 1 см на карте соответствует 2 км на местности, искомое расстояние будет 2 • 16 = 32 (км). При работе на карте 1:100 000 (где 1 см соответствует 1 км) полученное число сантиметров будет соответствовать такому же числу километров.

При отсутствии курвиметра для измерения кривых линий можно воспользоваться циркулем, применяя способ «шага», подобно тому, как это делается при измерении длинных линий.

На практике сотрудники МЧС измеряют расстояние на картах с помощью масштабной линейки, которая имеет шкалы для измерения расстояний на топографических картах среднего и мелкого масштабов. Так как на линейке имеются сантиметровые деления, то практически она пригодна для измерения расстояний на любых картах.

Поскольку с помощью циркуля расстояние определяется более точно, чем линейкой, можно воспользоваться циркулем и масштабной линейкой, используя последнюю в качестве линейного масштаба.

Измерить расстояние на карте онлайн

3planeta.com

С помощью этого сервиса вы можете определить суммарное расстояние между двумя или более точками на планете Земля, соединенных прямыми линиями. (Все точки нужно указывать щелчками).

Расстояние определяется в метрах и автоматически перекодируется в ярды. Как пример рассмотрено определение длины озера Лох-Несс в Шотландии.

mapsdirections.info

Выберите местоположение посредством нажатия на карту или использования поля поиска. Это позволит установить первый маркер. Нажмите снова на карту или введите другой объект поиска для установки второго маркера. Требуется как минимум два маркера для измерения расстояния и как минимум три маркера для измерения площади.

Все маркеры при необходимости можно перемещать на карте. Если вы допустили ошибку, нажмите на кнопку . Нажмите на кнопку , чтобы удалить все пункты с Google Карты и начать снова.

Результаты измерения расстояния будут указаны в метрах, километрах, футах, ярдах и милях. Результаты измерения площади будут указаны в квадратных метрах, квадратных километрах, квадратных футах, квадратных ярдах и акрах.

1. Как измерить расстояние между точками на Google Картах:
2. Откройте Google Карты на компьютере. Если для них включен упрощенный режим (обозначается значком молнии в нижней части экрана), то измерить расстояние нельзя.
3. Наведите курсор на начальную точку и нажмите правую кнопку мыши. Откроется меню.
4. Выберите Измерить расстояние.
5. Укажите на карте вторую точку, нажав левую кнопку мыши. Точно так же можно добавить ещё несколько точек.
6. При необходимости вы можете перетащить точку в другое место или удалить, нажав на нее.
7. На карточке в нижней части страницы будет указана общая протяженность пути в километрах и милях.
8. Когда закончите, нажмите на значок Закрыть.

Решение уравнений

Пример 1

Вычислить расстояние между прямой 3 + 4 — 6 = 0 и точкой M(-1, 3).

Решение

\(d\;=\;\;\frac{\left|3\times(-1)+4\times3-6\right|}{\sqrt{3^2+4^2}}=\frac{\left|-3+12-6\right|}{\sqrt{9+16}}=\frac{\left|3\right|}{\sqrt{25}}=\frac{\left|3\right|}5=0,6\)

Ответ: 0,6.

Пример 2

Найти расстояние между прямой 12 + 5 — 17 = 0 и точкой M(-3, 8).

Решение

\(d\;=\;\;\frac{\left|12\times(-3)+5\times8-17\right|}{\sqrt{12^2+5^2}}=\frac{\left|-36+40-17\right|}{\sqrt{144+25}}=\frac{\left|-13\right|}{\sqrt{169}}=\frac{\left|13\right|}{13}=1\)

Ответ: 1.

Пример 3

Вычислить расстояние между прямой 4 + 3 — 3 = 0 и точкой M(-2, 5).

Решение

\(d\;=\;\;\frac{\left|4\times(-2)+3\times5-3\right|}{\sqrt{4^2+3^2}}=\frac{\left|-8+15-3\right|}{\sqrt{16+9}}=\frac{\left|4\right|}{\sqrt{25}}=\frac{\left|4\right|}5=0,8\)

Ответ: 0,8.

Формула расчета расстояния по координатам

Пусть и являются географическими широтой и долготой двух точек 1 и 2, и — их абсолютная разность. Тогда , центральный угол между ними, определяется теоремой сферических косинусов:

Формула расстояние d т.е.длины дуги, для сферы радиуса R и приведены в радианах

Больше матиматики .

На компьютерных системах с низкой точностью с плавающей запятой, эта формула может иметь большие ошибки округления, если расстояние не большое (если две точки находятся в 1 км друг от друга на поверхности Земли, косинус центрального угла выходит 0,99999999). Для современных 64-разрядных чисел с плавающей запятой, формула Теоремы косинусов, которая приведенна выше, не имеет серьезных ошибок округления для расстояний более нескольких метров на поверхности Земли. Эта формула лучше подходит для вычисления растояние по координатам на небольшые расстояния

Для получения более точных рузультатов на большых расстояниях стараются исполтзовать формулу посложнее, в которой сделано предположение, что сфера является эллипсоидом с одинаковыми большой и малой осями.

Источник

Моя реализация на РНР

// Радиус земли
define('EARTH_RADIUS', 6372795);
 
/*
* Расстояние между двумя точками
* $φA, $λA - широта, долгота 1-й точки,
* $φB, $λB - широта, долгота 2-й точки
* Написано по мотивам http://gis-lab.info/qa/great-circles.html
* Михаил Кобзарев <mikhail@kobzarev.com>
*
*/
function calculateTheDistance ($φA, $λA, $φB, $λB) {
 
// перевести координаты в радианы
$lat1 = $φA * M_PI / 180;
$lat2 = $φB * M_PI / 180;
$long1 = $λA * M_PI / 180;
$long2 = $λB * M_PI / 180;
 
// косинусы и синусы широт и разницы долгот
$cl1 = cos($lat1);
$cl2 = cos($lat2);
$sl1 = sin($lat1);
$sl2 = sin($lat2);
$delta = $long2 - $long1;
$cdelta = cos($delta);
$sdelta = sin($delta);
 
// вычисления длины большого круга
$y = sqrt(pow($cl2 * $sdelta, 2) + pow($cl1 * $sl2 - $sl1 * $cl2 * $cdelta, 2));
$x = $sl1 * $sl2 + $cl1 * $cl2 * $cdelta;
 
//
$ad = atan2($y, $x);
$dist = $ad * EARTH_RADIUS;
 
return $dist;
}

Пример вызова функции:

$lat1 = 77.1539;
$long1 = -139.398;
$lat2 = -77.1804;
$long2 = -139.55;
 
echo calculateTheDistance($lat1, $long1, $lat2, $long2) . " метров";
// Вернет "17166029 метров"

Расчет расстояния между координатами

Данный сервис позволяет рассчитать расстояние между двумя точками с известными географическими координатами.

Как известно, кратчайшим расстоянием между двумя точками на земной поверхности является длина дуги круга, проведенного на сфере по этим двум точкам. При расчете расстояния по географическим координатам делается предположение, что Земля не плоская, а круглая (если быть точнее, имеет форму, приближенную к сфере), то есть Земля — сфероид.

Для определения расстояния между двумя точками будет применяться формула расчета длины дуги, так называемая «модифицированная формула гаверсинусов».

Поскольку в расчете участвует радиус, а у Земли, как у не совсем правильной сферы, он разный, скажем на северном полюсе — 6335.437 км, а на экваторе — 6399.592 км. В связи с этим в расчете берется среднее значение радиуса Земли равное 6372.795 км, что позволяет получать результат с точность 99,5%.

В калькуляторе ниже для примера приводится расчет расстояния между координатами г.Москва и г.Санкт-Петербург.

Расстояние Чебышёва (метрика шахматной доски)

Расстояние Чебышёва известно ещё как расстояние шахматной доски. Чтобы понять принцип такой метрики, нужно представить короля на шахматной доске — он может ходить во всех направлениях: вперёд, назад, влево, вправо и по диагонали.

Расстояние Чебышёва между двумя точками

Разница расстояния L1 и расстояния Чебышёва в том, что при переходе на одну клетку по диагонали в первом случае засчитывается два хода (например вверх и влево), а во втором случае засчитывается всего один ход.

Ещё эти оба расстояния отличаются от Евклидового расстояния тем, что у Евклидового движение по диагонали рассчитывается по теореме Пифагора.

Сравнение путей 3 метрик

Расстояние Чебышёва можно представить как проход по шахматной доске.

Вот ещё один пример представления расстояния Чебышёва. Допустим, у вас есть дрон с двумя независимыми моторами: первый мотор тянет дрон вперёд, второй — в сторону. Оба мотора могут работать одновременно и равномерно на максимуме своей мощности.

Поэтому дрон может передвинуться на одну клетку по диагонали так же быстро, как по горизонтали или вертикали.

Посмотрите ещё раз на карту города по расстоянию Чебышёва. Первый шаг — оба мотора работают одновременно, второй шаг идентичен первому, а на третьем шаге мотор, тянущий дрон вперёд, отключается, и дрон смещается в сторону.

Таким образом, расстояние Чебышёва определяется как самая большая дистанция на одной оси.

Пример расчёта расстояния Чебышёва между двумя точками

Прим. ред. Полученный результат является условным и некорректно сравнивать его с другими результатами.

Перевод статьи «3 distances that every data scientist should know»