Прямоугольная система координат на плоскости и в пространстве

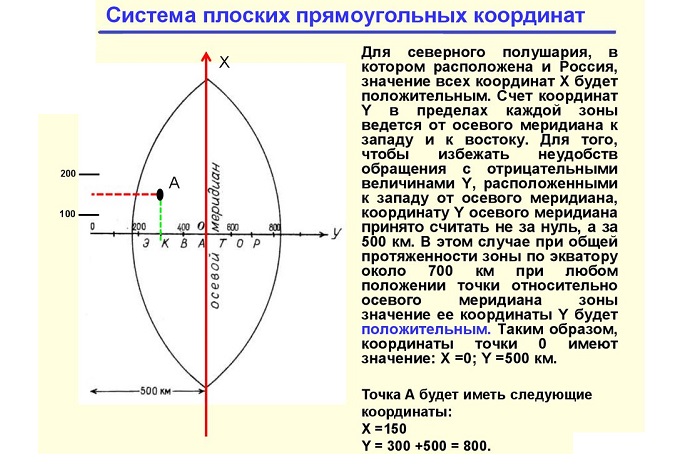
Система плоских прямоугольных координат

Для определения положения тел на земной поверхности можно использовать обычную прямоугольную СК.

Чтобы построить её центр и оси, необходимо учесть следующее:

1. В качестве исходной точки рассматривается центр масс нашей планеты.

2. Ось Z совпадает с осью вращения.

3. Ось X проходит через пересечение экваториальной плоскости, той, которая проходит через полюса и гринвичский географический меридиан и поверхности земного шара.

4. Y также проходит через экваториальную плоскость и поверхность планеты. Она перпендикулярна осям X и Z. Эта ось смотрит так, чтобы поворот от X к Y, если смотреть от Z, выполнялся бы против часовой стрелки.

Плоскую прямоугольную СК можно применять для местной топографической съёмки. В этом случае фиксируют перпендикулярные оси и устанавливают показатели, соответствующие расположению данной точки.

Прямоугольная декартова система координат

Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

А вот и координаты увлекательных уроков математики: на интерактивной платформе и в комфортном темпе! Запишите ребенка на бесплатный вводный урок в онлайн-школу Skysmart, чтобы закрыть пробелы по школьной программе и не бояться контрольных.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Определение прямоугольных координат на топографической карте

Чтобы осуществить определение координат  точек на картах, очень важно иметь ориентиры. Если изначальное координаты ясны и нужно лишь указать их на карте, то делается это следующим образом:

1. Определяется квадрат на сетке по километру координат.
2. При помощи линейки отсчитываются метровые величины внутри квадрата, сначала по параллельной линии к оси абсцисс, затем к оси ординат.
3. Вдоль линий указываются метровые значения.

В целом процедура завершена. Однако на практике не всё так просто. Зачастую не имеется значения изначальных координат

В таких случаях важно иметь определенные ориентиры, без которых найти точку представляется невозможным. В качестве ориентира может послужить любая близлежащая точка с известными координатами

Достаточно выяснить реальное расстояние между известной точкой и искомым объектом.

С другой стороны, современные технологии позволяют произвести точные измерения на месте с моментальным отображением результатов на электронной топографической карте. Для этого применяются методы лазерного измерения или радиолокации. В любом случае при практической необходимости выяснения местоположения того или иного объекта недвижимости правильным решением будет обратиться к специалистам.

В качестве специалистов могут выступать:

• инженеры государственной службы геодезии и картографии (кадастр);
• специалисты частных инженерных служб.

При этом частные инженерные службы в своём распоряжении имеют более высокотехнологичное, а значит и более точное оборудование, нежели государственные органы. Разумеется, услуги таких специалистов стоят не дёшево.

Геодезическая система координат

Данные, которые должны быть привязаны к определённому месту на земной поверхности, играют важную роль в различных сферах человеческой деятельности. 

Вот несколько примеров:

• при создании карт во время проведения топографической съёмки для отображения расположения предметов и их высот;

• для решения различных задач в навигации;

• при использовании спутниковых навигационных систем.

СК строится следующим образом:

1. Проводится плоскость через экватор (экваториальная).

2. Перпендикулярно ей рассматривается такая, которая проходит через нулевой меридиан.

3. Фиксируется расположение центра земли и полюсов.

Чтобы определить положение точки на Земле, к ней проводят отрезок, который перпендикулярен этому участку Земли. Обычно он отличается от того, который соединяется с центром планеты.

Строится сечение, проходящее через нормаль и полюса. Определяется угол, который она образует с проходящим через начальный геодезический меридиан. Таким образом определяется геодезический меридиан объекта.

Определяется ещё одно сечение, содержащее нормаль и оба полюса планеты. Здесь определяется линия пересечения с экваториальной. Теперь осталось определить угол между этой линией и нормалью, который равняется параллели этого места.

Положительные формы и расстояния

Ключевая идея геометрии положительных квадратичных форм, кратко ПКФ, состоит в том, что значение ПКФ f(x, y) есть квадрат длины вектора \(\overrightarrow{OA}\) или, что то же самое, есть квадрат расстояния от начала O до точки A с координатами (x, y).

Рассмотрим для примера две конкретные ПКФ:

f₁(x, y) = x2 + y2 и f₂(x, y) = x2 + xy + y2.

Сумма квадратов f₁(x, y) = x2 + y2 есть ПКФ и задает квадрат расстояния |OA| от начала O = (0, 0) до точки A = (x, y) в прямоугольной системе координат. Что касается формы f₂ = x2 + xy + y2, то ее положительность следует из того, что для ее коэффициентов оба неравенства a = 1 > 0 и \( ac − b^2 = 1 − \frac{1}{4} = \frac{3}{4} > 0 \) выполняются. Хотя это и не очевидно, форма f₂(x, y) также задает расстояние |OA|, но только если координаты (x, y) точки A рассматриваются относительно другой, вообще говоря не прямоугольной, системы координат, приспособленной к данной форме.

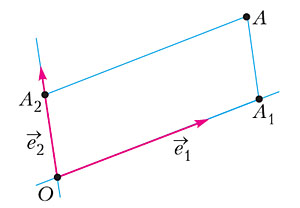
Произвольная система координат на плоскости задается упорядоченной парой векторов \( \{\overrightarrow{e_1}, \overrightarrow{e_2}\} \), исходящих из одной точки (начала O) и не лежащих на одной прямой (рис. 2). Такую пару векторов часто называют репером.

Векторы \( \overrightarrow{e_1} \) и \( \overrightarrow{e_2} \) определяют две прямые Oe₁ и Oe₂. Через точку A на плоскости проведем прямую, которая параллельна второй прямой Oe₂. Она пересекает прямую Oe₁ в некоторой точке A₁. Так как векторы \(\overrightarrow{OA}_1\) и \( \overrightarrow{e_1} \) коллинеарны, т.е. лежат на одной прямой, то для них имеем \(\overrightarrow{OA}_1 = x · \overrightarrow{e_1} \), где x — вполне определенное число, называемое координатой точки A₁ на прямой. Проведем через A прямую, параллельную первой прямой Oe₁. Она пересекает прямую Oe₂ в точке A₂. Точно так же, как и в первом случае, \(\overrightarrow{OA}_2 = y · \overrightarrow{e_2} \), а число y является координатой точки A₂ на прямой Oe₂. Упорядоченная пара чисел (x, y) и есть координаты вектора \(\overrightarrow{OA}\) (или координаты его конца — точки A) относительно репера \( \{\overrightarrow{e_1}, \overrightarrow{e_2}\} \).

Далее, форме f(x, y) = ax2 + 2bx + y2 сопоставим репер \( \{\overrightarrow{e_1}, \overrightarrow{e_2}\} \) такой, что

\( |\overrightarrow{e_1}|^2 = a,\quad |\overrightarrow{e_2}|^2 = c,\quad \overrightarrow{e_1} · \overrightarrow{e_2} = b.\) (3)

Напомним, что \( \overrightarrow{e_1} · \overrightarrow{e_2} \) означает скалярное произведение двух векторов, т.е. \( |\overrightarrow{e_1}| · |\overrightarrow{e_2}| · \text{cos}\:\angle\overrightarrow{e_1}\overrightarrow{e_2} \). Таким образом, по форме f(x, y) задается репер, у которого заданы длины его векторов и угол между ними. Тем самым репер задан однозначно с точностью до движения.

В частности, форме f₁(x, y) = x2 + y2 соответствует репер, задающий прямоугольную систему координат. А репер, соответствующий форме f₂(x, y) = x2 + xy + y2, состоит из единичных векторов \( \overrightarrow{e_1} \) и \( \overrightarrow{e_2} \) с углом 60° между ними, так как \( ( \overrightarrow{e_1} · \overrightarrow{e_2}) = \text{cos}\:\angle\overrightarrow{e_1}\overrightarrow{e_2} = b = \frac{1}{2} \).

Важно, что в системе координат репера, заданного в (3), квадрат длины отрезка OA равен значению формы f(x, y), где (x, y) — координаты точки A:

f(x, y) = |OA|2. (4)

Действительно, мы имеем

\( |OA|^2 = \overrightarrow{OA} · \overrightarrow{OA} = (x\overrightarrow{e_1} + y\overrightarrow{e_2})· (x\overrightarrow{e_1} + y\overrightarrow{e_2}) = x^2(\overrightarrow{e_1} · \overrightarrow{e_1} )
+ 2xy(\overrightarrow{e_1} · \overrightarrow{e_2}) + y^2(\overrightarrow{e_2} · \overrightarrow{e_2}) = ax^2 + 2bxy + y^2.\)

При выводе равенства (4) мы воспользовались тремя известными из школьной программы свойствами скалярного произведения векторов: свойствами распределительности, перестановочности и вынесения постоянного множителя.

Ориентация и руки

В двух измерениях

Правило правой руки

Фиксация или выбор оси x определяет направление оси y вверх. А именно, ось y обязательно является перпендикуляром к оси x через точку, отмеченную 0 на оси x . Но есть выбор, какую из двух половинных линий на перпендикуляре обозначить как положительную, а какую как отрицательную. Каждый из этих двух вариантов определяет различную ориентацию (также называемую хиральностью ) декартовой плоскости.

Обычный способ ориентирования плоскости с положительной осью x, направленной вправо, и положительной осью y, направленной вверх (при этом ось x является «первой», а ось y — «второй» осью), считается положительная или стандартная ориентация, также называемая правосторонней ориентацией.

Обычно используемая мнемоника для определения положительной ориентации — это правило правой руки . Поместите несколько замкнутую правую руку на плоскость с большим пальцем вверх, пальцы будут указывать от оси x к оси y в положительно ориентированной системе координат.

Другой способ ориентировать самолет — следовать правилу левой руки , положив левую руку на плоскость большим пальцем вверх.

Когда большой палец направлен от начала координат вдоль оси к положительному положению, кривизна пальцев указывает на положительное вращение вдоль этой оси.

Независимо от правила, используемого для ориентирования плоскости, вращение системы координат сохранит ориентацию. Переключение любой одной оси изменит ориентацию на обратную, но переключение обеих оставит ориентацию неизменной.

В трех измерениях

Рис. 7 — Левая ориентация показана слева, а правая — справа.

Рис. 8 — Правая декартова система координат с указанием координатных плоскостей.

После задания осей x и y они определяют линию, вдоль которой должна лежать ось z , но для этой линии есть два возможных направления. Возникающие в результате две возможные системы координат называются «правая» и «левая». Стандартная ориентация, при которой плоскость xy горизонтальна, а ось z направлена вверх (а оси x и y образуют положительно ориентированную двумерную систему координат в плоскости xy, если смотреть сверху на плоскость xy ) называется правосторонним или положительным .

Трехмерная декартова координатная стрелка

Название происходит от правила правой руки . Если указательный палец правой руки направлен вперед, средний палец согнут внутрь под прямым углом к ​​нему, а большой палец расположен под прямым углом к ​​обоим, три пальца указывают относительную ориентацию x -, y -, и z- оси в правой системе. Большой палец указывает ось x , указательный палец — ось y, а средний палец — ось z . И наоборот, если то же самое сделать левой рукой, получится система для левой руки.

На рисунке 7 изображены левая и правая системы координат. Поскольку трехмерный объект отображается на двухмерном экране, возникают искажения и неоднозначность. Оси направлены вниз (и справа) также означают точку к наблюдателю, в то время как «средний» ось предназначаются , чтобы указать расстояние от наблюдателя. Красный круг параллелен горизонтальной плоскости xy и указывает вращение от оси x к оси y (в обоих случаях). Следовательно, красная стрелка проходит перед г Оу.

Рисунок 8 — еще одна попытка изобразить правую систему координат. Опять же, возникает неоднозначность, вызванная проецированием трехмерной системы координат на плоскость. Многие наблюдатели видят рисунок 8 как «переворот» между выпуклым кубом и вогнутым «углом». Это соответствует двум возможным ориентациям пространства. Если смотреть на фигуру как выпуклую, это дает левую систему координат. Таким образом, «правильный» способ просмотра Рисунок 8 представляет себе представить х оси х , как указывает в сторону наблюдателя , и , таким образом , видя вогнутый угол.

Пространство Отсечения

После завершения работы вершинных шейдеров, OpenGL ожидает, что все координаты будут в определенном диапазоне, а всё что выходит за его границы будет отсечено. Отсеченные координаты отбрасываются, а оставшиеся становятся фрагментами, видимыми на экране. Вот откуда пространство отсечения получило своё название.

Задавать все видимые координаты значениями из диапазона на самом деле интуитивно непонятно, поэтому для работы мы определяем свой собственный набор координат и потом преобразовываем их обратно в NDC, как того ожидает OpenGL.

Для преобразования координат из пространства вида в пространство отсечения мы задаем так называемую матрицу проекции, которая определяет диапазон координат, например от -1000 до 1000 по каждой оси. Матрица проекции трансформирует координаты этого диапазона в нормализованные координаты устройства (-1.0, 1.0). Все координаты вне заданного нами промежутка не попадут в область , и, следовательно, будут отсечены. В том диапазоне, который мы задали матрицей проекции, координата (1250, 500, 750) не будет видна, так как её X-компонента выходит за границу, поэтому будет сконвертирована в значение, превышающее 1.0 в NDC, и, следовательно, вершина подвергнется отсечению.

Этот объем просмотра, задаваемый матрицей проекции, называется усечённой пирамидой (frustum) и каждая координата попадающая в эту пирамиду окажется и на экране пользователя. Весь процесс конвертации координат определенного диапазона в нормализованные координаты устройства (NDC), которые могут с легкостью отображены в двумерные координаты пространства вида, называется проецирование, так как матрица проекции проецирует 3D координаты на простые-для-преобразования-в-2D нормализованные координаты устройства.

Как только координаты всех вершин будут переведены в пространство отсечения, выполняется заключительная операция, называемая перспективное деление. В ней мы делим x,y и z компоненты вектора позиции вершины на гомогенную компоненту вектора w. Перспективное деление преобразует 4D координаты пространства отсечения в трехмерные нормализованные координаты устройства. Этот шаг выполняется автоматически после завершения работы каждого вершинного шейдера.

Именно после этого этапа, полученные координаты (используя установки glViewport) отображаются на координаты экрана и превращаются во фрагменты.

Матрица проекции преобразующая координаты вида в координаты отсечения может принимать две различных формы, и каждая форма определяет свою особенную усеченную пирамиду. Мы можем создать ортографическую матрицу проекции или перспективную.

Системы координат с более чем двумя измерениями

В трехмерном пространстве также есть третья ось, пространственная ось ( ось, здесь не показана), называемая аппликате (в географиикотэ ). В большинстве случаев оси — и — лежат в плоскости, а ось — используется для отображения высоты. Восемь частей пространства, образованных координатными плоскостями, называются октантами . Графически точки здесь образуют облако точек .
z{\ displaystyle z}Икс{\ displaystyle x}у{\ displaystyle y}z{\ displaystyle z}

Как и в двухмерном случае, в трехмерных геодезических системах координат оси — и — меняются местами, а ось — , как и в математической системе координат, направлена ​​вверх.
Икс{\ displaystyle x}у{\ displaystyle y}z{\ displaystyle z}

В обобщении математика предусматривает многомерные пространства (см .: 4D ). Например, ось расширения в четвертом пространственном измерении иногда упоминается как ось, направления расширения — как ана («вверху») и ката («внизу»).
ш{\ displaystyle w}

Прямоугольная система координат в трехмерном пространстве

Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.

Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.

Приложение к теореме Безу

Теорема Безу предсказывает, что количество точек пересечения двух кривых равно произведению их степеней (в предположении алгебраически замкнутого поля и с некоторыми соглашениями, которые следуют для подсчета кратностей пересечений). Теорема Безу предсказывает, что существует одна точка пересечения двух прямых, и в целом это верно, но когда прямые параллельны, точка пересечения бесконечна. В этом случае для определения точки пересечения используются однородные координаты. Точно так же теорема Безу предсказывает, что линия будет пересекать конику в двух точках, но в некоторых случаях одна или обе точки бесконечны, и для их определения необходимо использовать однородные координаты. Например, y = x 2 и x = 0 имеют только одну точку пересечения в конечной (аффинной) плоскости. Чтобы найти другую точку пересечения, преобразуйте уравнения в однородную форму, yz = x 2 и x = 0 . Это дает x = yz = 0 и, предполагая, что не все x , y и z равны 0, решения следующие: x = y = 0, z 0 и x = z = 0, y ≠ 0 . Это первое решение — точка (0, 0) в декартовых координатах, конечная точка пересечения. Второе решение дает однородные координаты (0, 1, 0), которые соответствуют направлению оси y . Для уравнений xy = 1 и x = 0 нет конечных точек пересечения. Преобразование уравнений в однородную форму дает xy = z 2 и x = 0 . Решение дает уравнение z 2 = 0, которое имеет двойной корень при z = 0 . Из исходного уравнения x = 0 , поэтому y ≠ 0, поскольку хотя бы одна координата должна быть ненулевой. Следовательно, (0, 1, 0) — точка пересечения, считая с кратностью 2 в соответствии с теоремой.

Математика. 6 класс

Конспект урока

Координатная ось. Часть 1

Перечень рассматриваемых вопросов:

Прямую, на которой выбрано начало отсчета, положительное направление и единичный отрезок, называют координатной осью.

Координатой точки A, лежащей на положительном луче координатной оси x, называется положительное действительное число х, равное длине отрезка OA. Координатой точки A, лежащей на отрицательном луче координатной оси x, называется отрицательное действительное число х, равное длине отрезка OA, взятой со знаком «–».

Координата начальной точки O равна нулю.

Теоретический материал для самостоятельного изучения

Прямую, на которой выбрано начало отсчёта, положительное направление и единичный отрезок, называют координатной осью.

Координатная ось может быть горизонтальной, вертикальной или направленной в любую удобную сторону. Положительное направление тоже может быть задано исходя из удобства работы в каждом конкретном случае.

Точка O делит ось на два луча: положительный и отрицательный.

Каждой точке координатной оси поставим в соответствие действительное число x по следующему правилу:

– начальной точке O – число нуль;

– точке A, находящейся на положительном луче, – число х, равное длине отрезка OA;

– точке A, находящейся на отрицательном луче, – отрицательное число х, равное длине отрезка ОА, взятой со знаком «–».

Определённую таким образом координатную ось называют координатной осью x, или, коротко, осью x.

Число, соответствующее любой точке оси, называют координатой этой точки.

Ранее вводилось понятие координатной оси, но на ней рассматривались только точки, имеющие рациональные координаты. Таким образом, ось была не полная и имела пустоты на месте иррациональных чисел.

Однако координата произвольной точки есть действительное число, т. е. оно может быть рациональным или иррациональным, как и длина отрезка, ему соответствующая.

Теперь координатная ось стала полной – каждой её точке соответствует действительное число.

Пусть А и В точки с координатами A(x) и B(y).

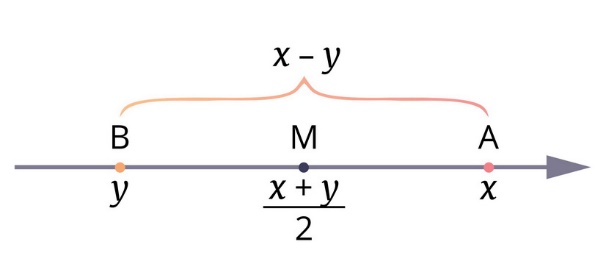
– если х > у, то точка A расположена правее точки B на координатной оси;

– расстояние между точками A и B равно х – у;

– середина отрезка AB – точка M – имеет координаты: (х+ у)/2.

Разбор заданий тренировочного модуля

Тип 1. Ввод с клавиатуры пропущенных элементов в тексте

Какая точка лежит правее?

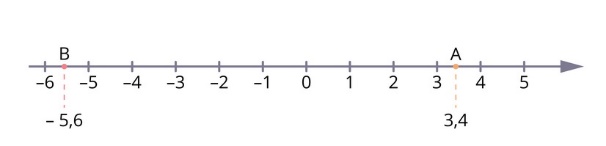
Найдём расстояние AB.

АВ = 3,4 – (– 5,6) = 3,4 + 5,6 = 9.

Тип 2. Единичный выбор

Найдём координаты точки М, середины отрезка АВ, если А(3,4) и В(– 5,6).

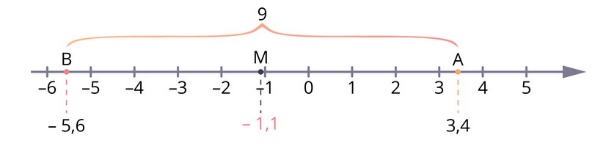
Варианты ответов: – 1,1; 1,1; 2,3; 6,8.

По формуле координаты середины отрезка получаем

Числовая ось

      Определение 1. Числовой осью (числовой прямой, координатной прямой)   Ox   называют прямую линию, на которой точка   O   выбрана началом отсчёта (началом координат) (рис.1), направление

O → x

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Рис.1

      Определение 2. Отрезок, длина которого принята за единицу длины, называют масштабом.

      Каждая точка числовой оси имеет координату, являющуюся вещественным числом. Координата точки   O   равна нулю. Координата произвольной точки   A ,   лежащей на луче   Ox ,   равна длине отрезка   OA .   Координата произвольной точки   A   числовой оси, не лежащей на луче   Ox ,   отрицательна, а по абсолютной величине равна длине отрезка   OA .

Другие проективные пространства

Использование действительных чисел дает однородные координаты точек в классическом случае реальных проективных пространств, однако может использоваться любое поле , в частности, комплексные числа могут использоваться для комплексного проективного пространства . Например, комплексная проективная линия использует две однородные комплексные координаты и известна как сфера Римана . Могут использоваться другие поля, в том числе конечные .

Однородные координаты для проективных пространств также могут быть созданы с элементами из тела (косое поле). Однако в этом случае необходимо учитывать тот факт, что умножение не может быть коммутативным .

Для общего кольца A , A проективное прямая над А может быть определена с однородными факторов , действующих на левой и проективной линейной группы , действующей справа.

Координаты геометрических объектов

Системы координат часто используются для определения положения точки, но они также могут использоваться для определения положения более сложных фигур, таких как линии, плоскости, круги или сферы. Например, координаты Плюккера используются для определения положения линии в пространстве. Когда есть необходимость, тип описываемого рисунка используется для различения типа системы координат, например, термин « координаты линии» используется для любой системы координат, которая определяет положение линии.

Может оказаться, что системы координат для двух разных наборов геометрических фигур эквивалентны с точки зрения их анализа. Примером этого являются системы однородных координат точек и прямых на проективной плоскости. Две системы в подобном случае называются дуалистическими . Дуалистические системы обладают тем свойством, что результаты одной системы могут быть перенесены в другую, поскольку эти результаты представляют собой лишь разные интерпретации одного и того же аналитического результата; это известно как принцип двойственности .