Системы координат

Метод координат (продвинутый уровень)

Мы с тобой продолжаем изучать метод координат. В прошлой части мы вывели ряд важных формул, которые позволяют:

• Находить координаты вектора;
• Находить длину вектора (альтернативно: расстояние между двумя точками);
• Складывать, вычитать векторы. Умножать их на вещественное число;
• Находить середину отрезка;
• Вычислять скалярное произведение векторов;
• Находить угол между векторами.

Конечно, в эти 6 пунктов не укладывается весь координатный метод.

Он лежит в основе такой науки, как аналитическая геометрия, с которой тебе предстоит познакомиться в ВУЗе. Я лишь хочу построить фундамент, который позволит тебе решать задачи ЕГЭ любого уровня сложности!

Этот раздел будет посвящен методу решения тех задач, в которых будет разумно перейти к методу координат. Эта разумность определяется тем, что в задаче требуется найти, и какая фигура дана.

Как найти на карте точку по долготе и широте

У любой точки на карте имеется уникальная географическая широта и долгота. Данные координаты позволяют определить местоположение без привязки к населенным пунктам, объектам и так далее. Современные сервисы с картами от Google или Yandex работают практически полностью в автоматическом режиме. Пользователю достаточно указать значения, а сайт самостоятельно покажет искомое место. Сегодня мы поговорим о том, как на карте найти точку по долготе и широте. Рассмотрим процедуру на примере карт от Google и Яндекс.

Google Карты

Популярный сервис карт от Google позволяет как осуществлять поиск по заданным координатам, так и определять координаты уже найденного географического объекта. Давайте разберемся, как осуществляются обе процедуры.

Найти точку на карте по долготе и широте с помощью Google можно следующим образом:

1. Зайдите на сайт с географическими картами.
2. Перейдите к поисковой строке. Сюда необходимо вписать или вставить координаты.
3. Если у вас уже есть точные данные местоположения, то просто вставьте их в строку и выберите найденный вариант. Google сам покажет нужную точку на карте.

Если вы хотите вручную ввести координаты, то выберите один из трех правильных вариантов:

• в формате градусов, минут и секунд;
• в формате градусов и десятичных минут;
• в десятичных градусах.

Пример каждого из вариантов представлен на скриншоте ниже.

Сначала указывается широта, а затем долгота. Помните, что в качестве разделительного знака перед десятичными знаками должна использоваться точка, а не запятая. Если вы впишете неправильные значения, то не найдете нужное место на карте.

Теперь разберемся, как можно узнать координаты той или иной точки. С помощью Google данная процедура выполняется крайне просто:

1. Отыщите нужное место на карте.
2. Кликните ЛКМ по точке один раз. В нижней части карты появится всплывающее окно с указанием названия места (город, область и прочее), а также с координатами.

1. Кликните по координатам. Они появятся в поиске. В окне информации появятся два варианта написания широты и долготы.

Полученные данные можно скопировать и использовать в своих целях. Еще один вариант поиска точки по координатам – это поисковая система от той же компании. Вам нужно всего лишь зайти в поисковик и вставить значения в строку, затем нажать Enter . Перед результатами поисковой выдачи появится блок с картой и отметкой. Кликните по ней, чтобы перейти к полной версии Google Карты.

Яндекс.Карты

Следующий популярный сервис с географическими картами также не лишен возможности поиска по широте и долготе. Единственное отличие в том, что при указании координат можно использовать сокращения с.ш./ю.ш. и в.д./з.д. вместо указания сторон света на английском языке. Поиск точки осуществляется следующим образом:

1. Зайдите на сайт карт от Яндекса.
2. В поисковую строку впишите координаты или вставьте их из буфера обмена Windows.
3. Осуществите поиск с помощью кнопки с иконкой лупы или клавиши Enter .
4. На карте появится точка местоположения указанных широты и долготы. В левой части указана информация о месте и координаты в другом формате.

Как и в случае с Google, рассмотрим порядок действий при нахождении координат какой-либо точки. Для этого кликните ЛКМ по месту на карте. Появится всплывающее окно, в котором нужно нажать на название места. Затем слева появится блок с информацией о географической позиции. Под названием и местоположением будут указаны координаты.

У пользователей есть и более быстрый способ поиска точек по координатам. Вам достаточно написать или вставить данные в поисковую строку на главной странице Яндекса. После этого появится поисковая выдача с блоком карты, на котором отмечена искомая точка.

Заключение

Итак, теперь вы умеете искать точки по долготе и широте. По схожему принципу работают и любые другие сервисы, приложения с картами. Поиск осуществляется автоматически, а от вас требуется лишь ввода широты и долготы с соблюдением всех правил.

Задавайте вопросы по теме через форму для комментариев. Мы ответим каждому пользователю, у которого возникли трудности!

Исходные данные для расчетов

Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.

По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:

– горизонтальные углы пунктов;

– измеренное расстояние между ними;

– координаты пункта ГГС или опорной сети;

– значение исходного дирекционного угла.

Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.

Координаты точки в декартовой системе координат на плоскости

Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равняется единственной точке М, расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии 2 от начала отсчета по положительному направлению, то она равна 2 , если -3, то соответственное расстояние 3. Ноль – это начало отсчета координатных прямых.

Иначе говоря, каждая точка М, расположенная на Ox, равна действительному числу xM . Этим действительным числом и является ноль, если точка M расположена в начале координат, то есть на пересечении Ox и Оу. Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.

Имеющееся число xM называют координатой точки М на заданной координатной прямой.

Возьмем точку как проекцию точки Mx на Ох, а как проекцию точки My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, где послучим соответственные точки пересечения  Mx и My .

Тогда точка Mx на оси Ох имеет соответствующее число xM , а My на Оу — yM. На координатных осях это выглядит так:

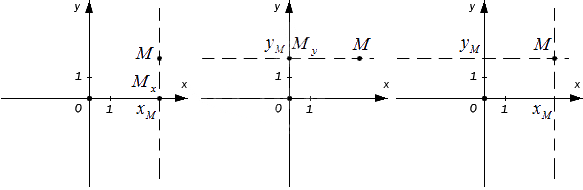
Каждая точка M на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел (xM, yM), называемую ее координатами. Абсцисса M – это xM , ордината M – это yM .

Обратное утверждение также считается верным: каждая упорядоченная пара (xM, yM) имеет соответствующую заданную в плоскости точку.

Метод треугольников на примере

1. Вычислить определитель: \( \left| {\begin{array}{*{20}{c}}2&3&{ – 1}\\{11}&{21}&{ – 5}\\4&6&9\end{array}} \right|\)

Давай разбираться, что мы складываем, а что – вычитаем.

Слагаемые, которые идут с «плюсом»:

Это главная диагональ: произведение элементов равно 

Первый треугольник, «перпендикулярный главной диагонали: произведение элементов равно 

Второй треугольник, «перпендикулярный главной диагонали: произведение элементов равно 

Складываем три числа: \( 378-60-66=252\)

Слагаемые, которые идут с «минусом»:

Это побочная диагональ: произведение элементов равно 

Первый треугольник, «перпендикулярный побочной диагонали: произведение элементов равно 

Второй треугольник, «перпендикулярный побочной диагонали: произведение элементов равно 

Складываем три числа:

\( -84+297-60=153\)Все, что осталось сделать – это вычесть из суммы слагаемых «с плюсом» сумму слагаемых «с минусом»:

\( 252-153=99\)Таким образом,

\( \left| {\begin{array}{*{20}{c}}2&3&{ – 1}\\{11}&{21}&{ – 5}\\4&6&9\end{array}} \right| = 99\)Как видишь, ничего сложного и сверхъестественного в вычислении определителей третьего порядка нет

Просто важно помнить про треугольники и не допускать арифметических ошибок. 

Координатная плоскость

Если построить на плоскости две взаимно перпендикулярные числовые оси: OX и OY, то они будут называться осями координат. Горизонтальная ось OX называется осью абсцисс (осью x), вертикальная ось OY — осью ординат (осью y).

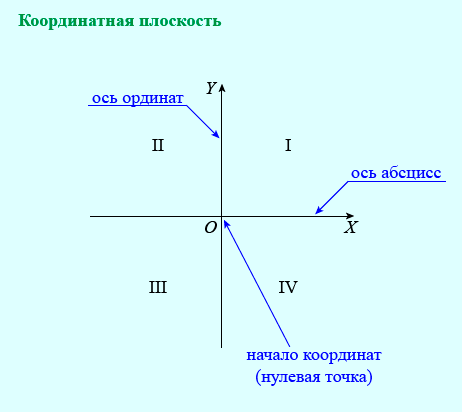
Точка O, стоящая на пересечении осей, называется началом координат. Она является нулевой точкой для обеих осей. Положительные числа изображаются на оси абсцисс точками вправо, а на оси ординат — точками вверх от нулевой точки. Отрицательные числа изображаются точками влево и вниз от начала координат (точки O). Плоскость, на которой лежат оси координат, называется координатной плоскостью.

Оси координат делят плоскость на четыре части, называемые четвертями или квадрантами. Принято эти четверти нумеровать римскими цифрами в том порядке, в котором они пронумерованы на чертеже.

Приравнивание функций друг к другу и нахождение корней

Выяснить, имеют ли точки пересечения графики функций, можно путем сравнения соответствующих тождеств и решения уравнения. Однако при этом допускается получение различных равенств с неизвестными. Тогда целесообразно воспользоваться специальными методиками.

Когда уравнение относится к первой степени или является линейным, решение получить достаточно просто. Метод заключается в переносе переменных величин в одну часть уравнения, а известных – в другую. Алгоритм действий:

• раскрытие скобок, приведение подобных коэффициентов;
• перенос членов с неизвестными в одну сторону, а с известными – в другую;
• математические преобразования;
• определение корня.

Квадратные уравнения решают с помощью одного из способов:

• разложение на множители;
• выделение полного квадрата;
• поиск дискриминанта;
• теорема Виета.

В первом случае представляется возможным понизить степень при неизвестной величине. Второй метод заключается в выделении квадрата по одной из формул сокращенного умножения. Каждая из этих методик реализуема при наличии знаний соответствующих тождеств, в том числе правил разложения на множители.

Третий способ состоит в поиске корней через дискриминант (Д), который является дополнительным параметром, позволяющим сразу решить задачу. Дискриминант определяется с помощью формулы:

\((-S)^2-4PU\)

В том случае, когда Д>0, переменная может иметь пару значений, которые превращают равенство в справедливое тождество. Если Д=0, то корень является единственным. Когда Д<0, искомое тождество с неизвестными не имеет решений.

Квадратные уравнения решают таким образом:

• выполнение необходимых алгебраических преобразований, в том числе раскрытие скобок и приведение подобных слагаемых;
• выбор наиболее оптимального способа решения и его реализация;
• проверка корней с помощью их подстановки в начальное выражение.

Примечание

Распространенной ошибкой является пренебрежение проверкой результатов решения. Некорректные действия могут привести к образованию ложных корней.

Существует несколько методик решения тождеств кубического и биквадратного типов:

• понижение степени, то есть разложение на множители;
• замена переменной.

Первый вариант решения подразумевает выполнение преобразований для последующего применения одной из формул сокращенного умножения. Такой способ применяют нечасто. Второй способ состоит в том, что при решении необходимо ввести переменную с более низкой степенью, которая упрощает выражение. Порядок действий при этом следующий:

• выполнение математических преобразований;
• выражение переменной через другую;
• решение квадратного или линейного уравнения;
• подстановка промежуточных корней, которые получилось найти на третьем шаге, во второй;
• вычисление искомых корней;
• проверка;
• исключение ложных решений;
• запись ответа.

# 3: решите, использовать формулы или нет

Если вам удобнее использовать формулы, чем использовать чуть более растянутые приемы, тогда решите: сейчас же запоминать формулы. Помните, что неправильное запоминание формулы хуже, чем не запоминание ее вообще, поэтому убедитесь, что вы запомнили и практиковали свои знания формул в период между настоящим моментом и днем ​​теста, чтобы закрепить это в своей голове.

Если, однако, вы предпочитаете посвятить свои учебные усилия чему-то другому (или вы просто чувствуете, что не запомните формулу правильно в день теста), тогда забудьте о них. Используйте теорему Пифагора вместо запоминания формулы расстояния и полностью вымойте руки над запоминанием.

Существует несколько способов решения большинства математических задач SAT, поэтому ваш выбор должен наилучшим образом соответствовать вашим личным сильным и слабым сторонам.

Изображение: ljphillips34 / Flickr

Прямоугольная система координат в трехмерном пространстве

Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.

Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.

Откуда берем данные и чем ищем по географическим объектам

Подступаясь к задаче, мы изучили готовые решения: где взять справочник координат с адресами и как потом искать по этому справочнику географические объекты. Оказалось, за нужными инструментами даже не придется далеко ходить.

Адресные объекты получаем из ФИАС — Федеральной информационной адресной системе. Это самый полный из открытых и официальных адресных справочников. Подробно о нем мы писали на «Хабре», а для этого материала важны четыре факта:

в ФИАС хранятся все адресные объекты страны, от регионов и ниже — до зданий и дополнительных территорий;
справочник свободно доступен в форматах DBF и XML;
ФИАС не идеален — в нем отсутствуют десятки тысяч домов и множество улиц, особенно новых;
каждому адресному объекту в справочнике соответствует уникальный ID — ФИАС-код

Код объекта иногда меняют, но для нашей статьи это не так важно.. Адресные объекты, загруженные из ФИАС вместе с ID, — основа нашего справочника для обратного геокодирования

Адресные объекты, загруженные из ФИАС вместе с ID, — основа нашего справочника для обратного геокодирования.

Координаты загружаем из OpenStreetMap (OSM). OSM — проект со свободной лицензией: энтузиасты собирают координаты всевозможных объектов и выкладывают для всех желающих.

Если по-простому, OSM — это набор точек, линий и полигонов на карте. У каждого объекта свое описание, тип и набор геокоординат.

Полигоны — это многоугольники, ограничивающие площади на карте. Они состоят из связанного набора точек с координатами. Полигонами обозначают границы регионов, районов, городов и даже зданий

Данные OSM для России лежат по адресам needgeo.com, osm.sbin.ru/osm_dump/ и osmosis.svimik.com/latest/.

Список источников публикуют на специальной странице в «Вики» проекта

Выгрузки состоят из PBF-файлов — этот формат используют вместо XML как более компактный. Превратить PBF в OSM XML ничего не стоит, с конвертацией справится куча одобренных сообществом утилит.

Для собственного справочника мы берем адресные объекты из ФИАС, а затем ищем их координаты в OSM. Если нашли, сохраняем объединенные данные. В итоге получаем такое пересечение ФИАС и OSM.

И все это замечательно, но есть одна проблема: с качеством данных в OSM дела обстоят непросто. Координаты объектов часто не соответствуют реальности.

Полигоны для регионов и районов адекватны. А для городов и ниже — уже не очень.

Поэтому основная работа, и с большой форой — это собрать из OSM адекватные данные и отсеять брак. Задача настолько объемная, что я отвел под нее в статье отдельный раздел.

Дома, которых нет в ФИАС, загружаем тоже из OSM. Выше я уже говорил, что в ФИАС отсутствуют десятки тысяч домов. Это даже не проблема, а просто реальность, фон. Поэтому мы пополняем свой справочник домами из OSM. Но только теми, для которых в ФИАС существует улица.

Разумеется, у пришедших из OSM зданий нет ФИАС ID. Поэтому мы идентифицируем их как ФИАС-код родителя + номер дома.

По справочнику ищем с помощью прекрасного Lucene — нашего многолетнего помощника. За наводку спасибо сведущему индийцу, написавшему пост Indexing Geographical Data With Lucene (хорошее дополнение — материал A dive into spatial search algorithms — о k-d-деревьях, на которых построен алгоритм поиска).

Как только мы узнали об у́дали Lucine, проблема с поиском решилась почти сама. Делов осталось — пройтись наждачкой.

1. Загрузили в Lucene свой справочник координат и адресов, получили индекс. Для легкости убрали из него почти все, оставив лишь ID адресов и координаты.
2. Наладили поиск по индексу: на вход — координаты, на выход — ID найденных адресных объектов. Другой информации поиск не возвращает, поскольку индекс мы донельзя скукожили.
3. Насытили выдачу, загружая из «большого» ФИАС данные по найденным ID. Добавляем много всего, от нужного всем адреса одной строкой до признака столицы региона у городов.
4. Придумали, как сортировать и отдавать полученные объекты.

Пока все выглядит просто, но это лишь малая часть работы. Никакого поиска адреса по координатам не получилось бы, не собери мы приличный справочник.

Прямоугольная декартова система координат

Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Правила координат:

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Декартова прямоугольная система координат.

Общие декартовы системы координат используются реже, чем специальный класс таких систем — декартовы прямоугольные системы координат.

Определение.

Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны единице. Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.

Нетрудно проверить, что координаты точки относительно декартовой прямоугольной системы координат в пространстве по абсолютной величине равны расстояниям от этой точки до соответствующих координатных плоскостей. Они имеют знак плюс или минус в зависимости от того, лежит точка по ту же или по другую сторону от плоскости, что и конец базисного вектора, перпендикулярного этой плоскости.

Аналогично находят координаты точки относительно декартовой прямоугольной системы координат на плоскости.

Вычисление расстояния от прямой до плоскости

На самом деле, здесь нет ничего нового. Как могут располагаться прямая и плоскость друг относительно друга?

У них есть всего \( 2\) возможности: пересечься, или прямая параллельна плоскости. Как ты думаешь, чем равно расстояние от прямой до плоскости, с которой данная прямая пересекается?

Мне кажется, что тут ясно, что такое расстояние равно нулю. Неинтересный случай.

Второй случай хитрее: тут уже расстояние ненулевое. Однако, так как прямая параллельна плоскости, то каждая точка прямой равноудалена от этой плоскости:

Таким образом:

Расстояние от плоскости до параллельной ей прямой равно расстоянию от любой точки прямой до плоскости.

А это значит, что моя задача свелась к предыдущей: ищем координаты любой точки на прямой, ищем уравнение плоскости, вычисляем расстояние от точки до плоскости.

На самом деле, такие задачи в ЕГЭ встречаются крайне редко. Мне удалось найти лишь одну задачу, и то данные в ней были такими, что метод координат к ней был не очень-то и применим!

Теперь перейдем к другому, гораздо более важному классу задач:

Определение точек на карте по координатной сетке

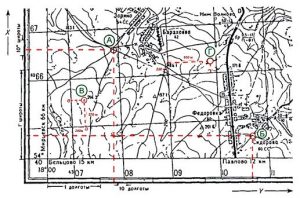Координатную сеть иначе ещё называют километровой, так как на мелких картах величина квадратов сетки равняется километру. На подобных картах километровая сеть изображается в виде линий, прочерченных параллельно осями и имеющих определённый интервал между собой. Интервал устанавливается в зависимости от масштаба.

Так, при масштабе 1 : 25 000 значение интервала равняется 4 сантиметрам. При большем масштабе интервал не бывает меньше 2 сантиметров, невзирая на реальное расстояние между линиями. При масштабе больше чем 1 : 500 000 сетка прямо не изображается. Обозначаются лишь выходные метки по краям карты.

Координатная сеть является условной для отдельной зоны, и для сопоставления топографии соседних зон по краям карты оставляются отметки сетки, которые соответствуют выходам сетки соседней зоны.

При обозначении значений координат на топографических картах координатная сеть позволяет быстрее обозначить необходимую точку. Отсчет расстояния идёт от границ квадрата координатной сетки. Каждая из сторон отдельного квадрата сетки имеет заранее определенную реальную длину в километрах (1, 2 и т. д. километров).

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Выводы

Понимание координатной плоскости и того, как точки помещаются в нее, являются основными строительными блоками для координатной геометрии. Обладая этим пониманием, вы сможете выполнять более сложные задачи координатной геометрии, такие как поиск склонов и вращающиеся формы.

Координатная геометрия не является незначительной частью математического раздела SAT, но, к счастью, успех в основном зависит от организации и усердия. Будьте осторожны, отслеживая свои негативы и все свои движущиеся части, и вы сможете доминировать над этими точечными вопросами и всей координатной геометрией, которую SAT может вам бросить.