Формула скорости

Содержание:

В Евклидово расстояние положительное число, которое указывает на разделение между двумя точками в пространстве, где выполняются аксиомы и теоремы геометрии Евклида.

Расстояние между двумя точками A и B в евклидовом пространстве — это длина вектора AB принадлежащей единственной линии, проходящей через эти точки.

Пространство, которое люди воспринимают и куда мы движемся, представляет собой трехмерное пространство (3-D), в котором выполняются аксиомы и теоремы геометрии Евклида. В этом пространстве содержатся двумерные подпространства (плоскости) и одномерные подпространства (линии).

Евклидовы пространства могут быть одномерными (1-D), двумерными (2-D), трехмерными (3-D) или n-мерными (n-D).

Точки в одномерном пространстве X — это те, которые принадлежат ориентированной прямой (OX), направление от O к X — положительное направление. Для определения местоположения точек на указанной линии используется декартова система, которая заключается в присвоении номера каждой точке линии.

Расстояние и скорость

Положение каждой физической точки можно описать с помощью координатных осей. Другими словами, системой, которая по отношению к исследуемому телу остаётся неизменной. Изменение положения относительно другого объекта можно представить пройденным расстоянием. Фактически это путь, для которого известно начало и конец. С физической точки зрения, расстояние — величина, являющаяся размерностью длины, и выражающаяся в её единицах.

В математике мера пройденного пути тесно связана с метрическим пространством, то есть положением, где существует пара (x, d), определённая в декартовом произведении. Соответственно, если координату принять за x, y, можно сказать следующее:

• начало пути и его конец обозначают точками с координатами d (x, y) и p (x, y);
• пройденное расстояние можно определить, отняв из конечных координат начальные;
• изменение положения будет нулевым, когда d = p.

В физике расстояние измеряют единицами длины. В соответствии с СИ за размерность берут метр. Расстояние — мера пройденного пути, то есть длина. Если необходимо просто определить изменение положения без учёта, когда и как оно произошло, используют координатные оси. Но при нахождении пройденного пути за время в формуле для расстояния должна учитываться ещё одна величина — скорость.

Обозначают эту характеристику символом V. Характеризует она быстроту перемещения в выбранной системе отсчёта. По определению скорость равняется производной радиус-вектора точки по времени. Иными словами, это значение, задающееся положением в пространстве относительно неизменной координаты, за которую чаще всего принимается начало.

Но на самом деле не всё так однозначно. Скорость необязательно должна быть одинаковой на всём пути. На определённых промежутках она может увеличиваться или уменьшаться, поэтому в математике под её значением понимают среднюю величину. Считается, что тело движется равномерно при прохождении установленного расстояния.

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения x(t) = x0 + v0xt + axt^2/2 x(t) — искомая координата x0 — начальная координата v0x — начальная скорость тела в данный момент времени [м/с] t — время ax — ускорение [м/с^2]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости →          → v = v0 + at → v — конечная скорость тела [м/с] v0 — начальная скорость тела [м/с] t — время → a — ускорение [м/с^2]

Задача

Найдите местоположение автобуса через 0,5 часа после начала движения, разогнавшегося до скорости 60 км/ч за 3 минуты.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

v = v0 + at
a = v — v0 / t

Так как автобус двигался с места, v0 = 0. Значит
a = v/t

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч^2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt^2/2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

x(t) = axt^2/2

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
x = 1200*0,5^2/2 = 1200*0,522= 150 км

Ответ: через полчаса координата автобуса будет равна 150 км.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

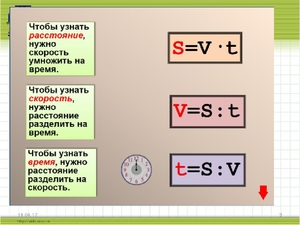
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Понятие о времени

Существует характеристика, с которой приходится сталкиваться каждый день вне зависимости от возраста, социального статуса, различных способностей и умений. С её помощью определяют будущее, прошедшее и настоящее. По сути, это маркер, определяющий событие. Называют его временем. Рассматривая движение, всегда учитывают эту характеристику, как и её прогрессию.

Время является частью пространственной координаты. Но если относительно других осей можно перемещаться в различных направлениях, относительно него движение определяется только вперёд или назад. Неотъемлемой частью, связанной со временем, является пространство, благодаря которому и возможно понять суть параметра.

Исследованием характеристики занимались философы и учёные в различные периоды существования человечества. Видеть и слышать время невозможно, в отличие от осязаемого пространства, которое возможно наблюдать сразу и везде. Причём в нём можно перемещаться.

Сегодня так и нет ответов на следующие вопросы о времени:

В классической физике для определения временного изменения используется специальная координата пространство-время. Принято будущие события обозначать знаком плюс, а прошедшие минусом. Единица измерения времени связана с вращением планеты вокруг своей оси и Солнца. Этот выбор был сделан условно и привязан к удобству жизнедеятельности человечества.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

1. Справочный портал «Калькулятор».
2. Allcalc.
3. Fxyz.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Расстояние в зависимости от направленного расстояния и смещения

Расстояние по пути по сравнению со смещением

И расстояние, и смещение измеряют движение объекта. Расстояние не может быть отрицательным и никогда не уменьшается. Расстояние — это скалярная величина или величина , тогда как смещение — это векторная величина, имеющая как величину, так и направление . Он может быть отрицательным, нулевым или положительным. Направленное расстояние не измеряет движение; он измеряет расстояние между двумя точками и может быть положительным, нулевым или отрицательным вектором.

Расстояние , пройденное транспортным средством (например , в виде записанного с помощью одометр ), человека, животного или объекта вдоль изогнутой траектории от точки А до точки Б , следует отличать от прямолинейного расстояния от A до B . Например, независимо от расстояния, пройденного за время пути от A до B и обратно до A , смещение равно нулю, поскольку начальная и конечная точки совпадают. В общем, расстояние по прямой не равно пройденному расстоянию, за исключением поездок по прямой.

Направленное расстояние

Направленные расстояния можно определять по прямым и изогнутым линиям.

Направленные расстояния вдоль прямых линий — это векторы, которые определяют расстояние и направление между начальной и конечной точками. Направленное расстояние точки C от точки A в направлении B на прямой AB в евклидовом векторном пространстве — это расстояние от A до C, если C падает на луч AB , но является отрицательным для этого расстояния, если C падает на луч BA (т. е. если C не находится на той же стороне от A, что и B ). Например, направленное расстояние от флагштока Главной библиотеки Нью-Йорка до флагштока Статуи Свободы:

• Отправная точка: флагшток библиотеки
• Конечная точка: статуя флагштока.
• Направление: -38 °
• Расстояние: 8.72 км

Другой вид направленного расстояния — это расстояние между двумя разными частицами или точечными массами в данный момент времени. Например, расстояние от центра тяжести Земли A до центра тяжести Луны B (что не означает строго движение от A к B ) попадает в эту категорию.

Направленное расстояние вдоль изогнутой линии не является вектором и представлено сегментом этой изогнутой линии, определяемой конечными точками A и B , с некоторой конкретной информацией, указывающей смысл (или направление) идеального или реального движения от одной конечной точки сегмент к другому (см. рисунок). Например, простая маркировка двух конечных точек как A и B может указывать на смысл, если предполагается упорядоченная последовательность ( A , B ), что подразумевает, что A является начальной точкой.

Смещение

Смещение (см. Выше) — это особый вид направленного расстояния, определенный в механике . Направленное расстояние называется смещением, когда это расстояние по прямой (минимальное расстояние) от A и B , и когда A и B — позиции, занятые одной и той же частицей в два разных момента времени. Это подразумевает движение частицы. Расстояние, пройденное частицей, всегда должно быть больше или равно ее смещению, причем равенство имеет место только тогда, когда частица движется по прямой траектории.

Какое же оно – расстояние?

В физике у каждой физической величины имеется свой символ (обозначение или на латинице, или греческой буквой). Все это сделано для того, чтобы было проще и не путаться. Согласитесь, можно замучиться при написании в тетрадь примерно такой фразы: расстояние = скорость х время. А в физике очень и очень много различных формул с множеством параметров. Причем встречаются и квадратные, и кубические величины. Так какой буквой обозначается расстояние в физике? Сразу оговоримся, что встречаются двух видов обозначения, так как расстояние и длина имеют одинаковые величины и одни и те же единицы измерения. Итак, «S» — это то самое обозначение. Встретите такую букву в задачках или формулах из раздела «Механика».

Поверьте, в решении задач нет ничего сложного. Но при условии, что вы знаете математику и успеваете по ней. Вам понадобятся знания по операциям с дробями, умение считать, раскрывать скобки, решать уравнения. Без таких навыков по физике будет очень сложно.

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

t = S: V

15: 3 = 5 (с)

Составим выражение: 5 3: 3 = 5 (с) Ответ: 5 с потребуется слепню.

Реши задачу.

1. Катер, двигаясь со скоростью 32 км/ч, про­шёл путь между пристанями за 2 ч. Сколько потребуется времени, чтобы пройти этот же путь на лодке, если она движется со скорос­тью 8 км/ч?

2.Велосипедист, двигаясь со скоростью 10 км/ч, проехал путь между деревнями за 4 ч. Сколько

потребуется времени пешеходу, чтобы пройти этот же путь, если он движется со скоростью 15 км/ч?

Составные задачи на время. II тип.

Образец:

Многоножка сначала бежала 3 мин со скоростью 2 дм/м, а потом она побежала со скоростью 3 дм/м. За какое время мно­гоножка пробежала оставшийся путь, если всего она пробежала 15 дм? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.

Скорость (V) Время (t) Расстояние (S)

С. — 2 дм/мин З мин?дм

П.-3 дм/мин? ? мин?дм 15дм

Составим план решения этой задачи. Что­бы узнать, время многоножки потом, надо узнать какое расстояние она пробежала потом, а для этого надо знать, какое рас­стояние она пробежала сначала.

t п S п S с

S с = V с · t

2 3 = 6 (м) — расстояние, которое пробе­жала многоножка сначала.

S п = S — S с

15 — 6 = 9 (м) — расстояние, которое пробежала многоножка потом.

Чтобы найти время, надо расстояние раз­делить на скорость.

9: 3 = 3(мин)

Ответ: за 3 мин многоножка пробежала оставшийся путь.

Реши задачу.

1. Волк бежал по лесу 3 ч со скоростью 8 км/ч. По полю он бежал со скоростью 10 км/ч. Сколько времени волк бежал по полю, если он пробежал 44 км?

2. Рак до коряги полз 3 мин со скоростью 18 м/мин. Остальной путь он полз со скоростью 16 м/мин. Сколько времени потребовалось раку на остальной путь, если он прополз 118м?

3. Гена добежал до футбольной площадки за 48 с со скоростью 6 м/с, а потом он побежал к школе со скоростью 7 м/с. Через какое время Гена добежит до школы, если он пробежал 477 м?

4. Пешеход шёл до остановки 3 ч со скоростью 5 км/ч, после остановки он пошёл со скорос­тью 4 км/ч. Сколько времени пешеход был в пути после остановки, если он прошёл 23
км?

5. Уж плыл до коряги 10с со скоростью 8 дм/с, а потом он поплыл до берега со скоростью 6 дм/с. За какое время доплыл уж до берега, если он проплыл 122дм?

Составные задачи на скорость. I тип

Образец:

Из норки побежали два ёжика. Один бе­жал 6 с со скоростью 2 м/с. С какой ско­ростью должен бежать другой ёжик, чтобы преодолеть это расстояние за 3 с? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.

Скорость (V) Время (1) Расстояние (8)

I — 2 м/с 6 с одинаковое

II — ?м/с 3 с

Составим план решения этой задачи. Что­бы найти скорость второго ёжика, надо найти расстояние, которое пробежал пер­вый ёжик.

Чтобы найти расстояние, надо скорость умножить на время.

S = V I · t I

2 · 6 = 12 (м) – расстояние, которое пробежал первый ежик.

Чтобы найти скорость, надо расстояние разделить на время.

V II = S: t II

12:3 = 4(м/с)

Составим выражение: 2 6:3 = 4 (м/с)

Ответ; 4м/с скорость второго ёжика.

Реши задачу.

1. Один кальмар плыл 4 с со скоростью 10 м/с. С какой скоростью должен плыть другой кальмар, чтобы преодолеть это расстояние за 5 с?

2. Трактор, двигаясь со скоростью 9 км/ч, прошёл путь между деревнями за 2 ч. С какой скоростью должен идти пешеход, чтобы пре­одолеть это расстояние за 3 ч?

3. Автобус, двигаясь со скоростью 64 км/ч, про­шёл путь между городами за 2 ч. С какой скоростью должен ехать велосипедист, что­бы преодолеть это расстояние за 8 ч?

4. Чёрный стриж летел 4 мин со скоростью 3 км/мин. С какой скоростью должна лететь утка кряква, чтобы преодолеть это расстоя­ние за 6 мин?

Составные задачи на скорость. II тип

Лыжник до горки ехал 2 ч со скоростью 15 км/ч, а потом по лесу он ехал ещё 3 ч. С какой скоростью лыжник будет ехать по лесу, если всего он проехал 66км?

В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.

Содержание урока

Решение задач

Чтобы уметь решать простые задания в средних классах по математике, связанных с движением, нужно знать всего одну формулу

При этом необходимо пристальное внимание уделять размерности. Все вычисления осуществляются в СИ

Вот некоторые из типовых заданий, используемые при обучении школьников в четвёртом классе средней школы:

Все задачи на движение можно разделить на несколько типов: перемещение навстречу, движение вдогонку, нахождение параметров относительно неподвижного объекта. Но, несмотря на их виды, все они решаются по одинаковому алгоритму, поэтому для удобства можно сделать памятку, указав в ней формулы и размерность величин.

Общая формула

Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:

Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).

Действительно, пусть имеется физическое тело, находящееся в каком-то месте

Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2)

В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.

Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.

FAQ (скорость):

Как вы рассчитываете скорость (с примером)?

Чтобы вычислить скорость, вы должны разделить расстояние на время, которое требуется, чтобы пройти то же самое расстояние, совсем на следующем, вы должны добавить к нему свое направление. Наш скоростной искатель также определяет скорость таким же образом.

Например:

Если вы проехали 50 миль в течение 1 часа, двигаясь на запад, то говорят, что ваша скорость составляет 50 миль в час на запад или 50 миль в час на запад.

Как вы находите скорость с расстоянием и временем?

Все, что вам нужно, чтобы вставить значения в вышеупомянутый калькулятор скорости и времени, чтобы найти скорость с расстоянием и временем.

• Прежде всего, вы должны нажать на «вкладку ускорения»
• Совсем скоро вы должны выбрать опцию «конечная скорость» из выпадающего меню финала конвертер скорости
• Затем вы должны ввести значение начальной скорости в указанное поле
• Сразу после этого вы должны ввести значение ускорения в данное поле

Наконец, вы должны ввести значение времени в указанное поле, затем, нажав кнопку «Рассчитать», калькулятор окончательной скорости мгновенно вычислит конечную скорость для заданных входных данных.

Может ли скорость быть отрицательной?

Непосредственно – да, скорость может быть отрицательной. Объект, который движется в отрицательном направлении, обозначен как отрицательная скорость. И, если объект ускоряется, то его ускорение – это то, что направлено в том же направлении, что и его движение (в таком случае это называется отрицательным ускорением).

Как найти начальную скорость?

Если вы хотите мгновенно рассчитать начальную скорость, то все, что вам нужно, это вставить значения в вышеуказанную начальную конвертер скорости. И, если вы хотите сделать это вручную, используйте приведенную ниже формулу начальной скорости:

Начальная формула скорости:

Начальная скорость = конечная скорость – (ускорение × время)

vi = vf – в

Читай дальше!

Прежде всего, вы должны выяснить, какое из смещения (S), конечной скорости (Vf), ускорения (A) и времени (T) вы должны решить для начальной скорости (vi)

• Если у вас есть Vf, A и T, то вы должны использовать Vi = Vf – AT
• Если у вас есть S, Vf и T, то вы должны использовать Vi = 2 (S / T) – Vf
• Если у вас есть S, Vf и A, то вы должны использовать Vi = квадратный корень из (Vf ^ 2 – 2AS)
• Если у вас есть S, A и T, то вы должны использовать Vi = (S / T) – (AT / 2)

Как найти конечную скорость?

Попробуйте приведенный выше финал калькулятор скорости, чтобы выполнить мгновенные вычисления. Если вы хотите сделать это самостоятельно, то вам следует использовать данную формулу окончательной скорости.

V = U + AT

S = UT + 1/2 AT ^ 2

V ^ 2 = U ^ 2 + 2AS

Читай дальше!

Прежде всего, выясните, какую из начальной скорости (U), времени ускорения (A) (T) и смещения (S) вы должны решить для конечной скорости.

• Если у вас есть U, A и T, то вы должны использовать V = U + AT
• Если у вас есть S, U и T, то вам следует попробовать V = 2 (S / T) – U
• Если у вас есть S, U и A, то вы должны использовать V = квадратный корень (U ^ 2 + 2AS)
• Если у вас есть S, A и T, то вы должны использовать V = (S / T) + (AT / 2)

Что вызывает изменение скорости?

Эксперты изображают, что силы – это то, что влияет на движение объектов – они могут вызывать движение, также они могут останавливаться, замедляться или даже изменять направление движения объекта калькулятор скорости. Поскольку сила вызывает изменения в скорости или направлении объекта, говорят, что силы вызывают изменения в скорости. Помните, что ускорение называется изменением скорости.

Конец Примечание:

Имейте в виду, что скорость зависит от расстояния, а когда речь идет о скорости, она зависит от смещения – несомненно, эти две величины фактически одинаковы (даже имеют одинаковую величину), когда интервал времени мал. Используйте вышеупомянутый инструмент, чтобы понять, как вычислить скорость и даже решить ваши физические уравнения в мгновение ока!

Other Languages: Velocity Calculator, Hız Hesaplama, Kalkulator Prędkości, Geschwindigkeit Berechnen, 時速計算, Výpočet Rychlosti, Calculo De Velocidade, Calcul Vitesse, Calcular Velocidad, Calcolo Velocità, 속도 계산기, Kalkulator Kecepatan, حاسبة السرعة, Nopeuslaskin

Задачи на встречное движение

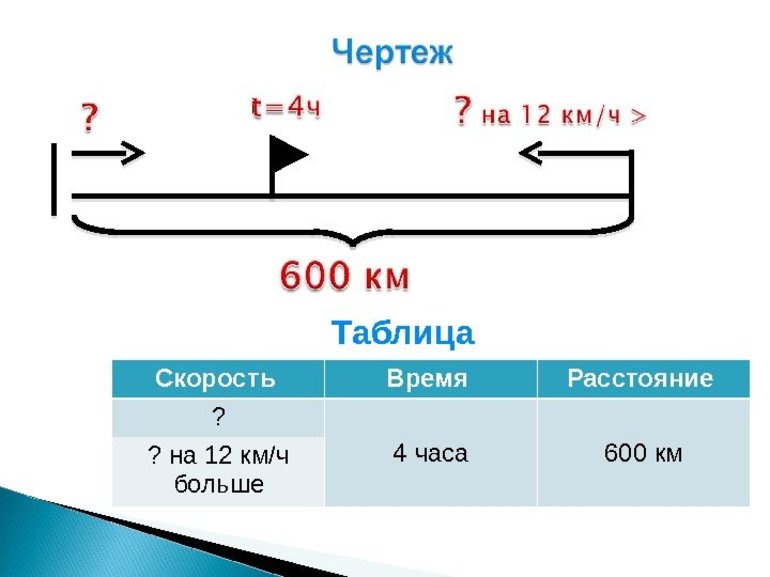
В таких задачах два объекта движутся навстречу друг другу. Задачи на встречное движение можно решать двумя способами: 1. Найти значения скорости, времени и расстояния для каждого объекта.2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Задача 4.

Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?Решение: Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные: 80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд, 240+210=450 (км) – проехали два поезда.Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние: 80+70=150 (км/ч), 150*3=450 (км).Ответ: города находятся на расстоянии 450 км.

Задача 5.

Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?Решение: Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус, 160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.Ответ: Через 2часа расстояние между автобусами будет 150 км.

Какой буквой обозначается скорость?

В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Когда такая связь существует, это обозначено в скобках.

В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Диакритические знаки добавляются к символу физической величины для обозначения определённых различий.

Формула дистанции

Имея полученные представления и знания о свойствах точек и векторов, можно перейти к вопросу нахождения формулы расстояния. Согласно геометрическому определению, под дистанцией между двумя точками понимают длину отрезка, который их соединяет. Эта величина также равна модулю вектора, построенного на нульмерных объектах.

Длину направленного отрезка на плоскости определить просто: необходимо возвести в квадрат каждую его координату, сложить полученные значения, и взять квадратный корень из результирующей суммы. Для вектора a- (x; y) длина будет равна следующей величине:

Возведение суммы в степень 0,5 эквивалентно взятию из нее квадратного корня.

Поскольку определение координат вектора по соответствующим значениям точек известно, можно получить следующую простую формулу для A (x1; y1) и B (x2; y2):

В трехмерном пространстве соответствующее выражение будет иметь подобную форму, только добавится третья координата z.

Как найти расстояние, если известно время и скорость?

Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:

Решение задачи: Записываем в черновик, что нам известно из условия задачи:

Скорость Зайца — 1 километр за 1 минуту

Время, которое Заяц бежал до норы — 3 минуты

Расстояние — неизвестно

Теперь, то же самое запишем математическими знаками:

v — 1 км/мин

 t — 3 минуты

S — ?

Вспоминаем формулу для нахождения расстояния:

S = v ⋅ t 

Теперь запишем решение задачи цифрами:

S = 3 ⋅ 1 = 3 км

Может быть, они умеют дружить?

Как научиться решать более сложные задачи?

Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.

Ребенок, который умеет решать задачи, может гордиться собой

Единицы измерения

Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.

Единицы измерения для решения задач про скорость, время и расстояние

Для любознательных: Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.

Единицы измерения

Задача про удава: Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд.  Какова длина удава? (решение под картинкой)

Как узнать длину удава?

Решение: 

Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.

Запишем эти данные:

Скорость мартышки — 60 см/сек

Скорость слоненка — 20 см/сек

Время — 5 секунд

Расстояние неизвестно

Запишем эти данные математическими знаками:

v1 — 60 см/сек

v2 — 20 см/сек

t — 5 секунд

S — ?

Запишем формулу для расстояние, если известна скорость и время:

S = v ⋅  t 

Посчитаем, какое расстояние прошла мартышка:

S1 = 60 ⋅ 5 = 300 см

Теперь посчитаем, сколько прошел слоненок:

S2 = 20 ⋅ 5 = 100 см

Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:

S = S1 + S2 = 300 + 100 = 400 см

ВИДЕО: Задачи на движение

Мы будем учиться решать задачи на нахождение скорости движения по данному расстоянию и времени. Сравните скорость Зелибобы и Кубика. ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, служащие для записи математических понятий, предложений и выкладок.

Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.

Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Поскольку скорость света в вакууме – величина постоянная, в расчетах она принимается за константу. Скорость это величина, которая характеризует быстроту перемещения объекта относительно выбранной системы отсчета.